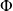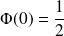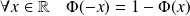Lois continues usuelles
On considère toujours un espace probabilisé
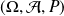dont l'univers
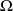n'est pas dénombrable.
Définition :
Une variable aléatoire
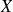suit la loi uniforme sur l'intervalle
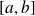si elle admet une densité
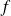telle que :
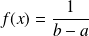si
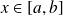et
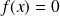sinon.
On note
.
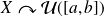Son espérance est
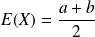et sa variance est
.
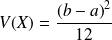La fonction de répartition est :
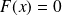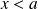
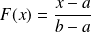si
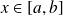
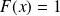si
si
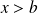
Définition :
Une variable aléatoire
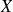suit la loi exponentielle de paramètre
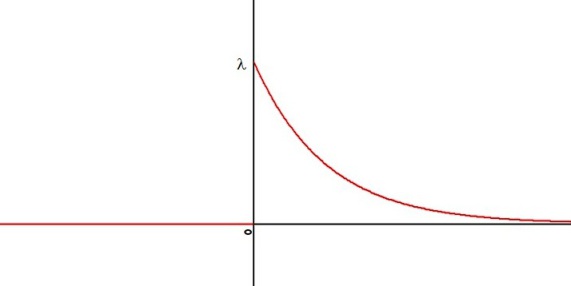
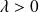si elle admet une densité
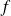telle que :
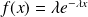si
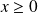et
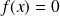sinon.
On note
.
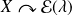Son espérance est
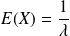et sa variance est
.
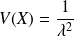La fonction de répartition est :
-
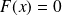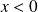
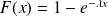si
si
.
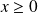Cette loi modélise la durée de vie d'un phénomène sans mémoire : sa durée de vie à partir d'un instant ne dépend pas du temps qui s'est écoulé avant cet instant.
Définition :
Une variable aléatoire
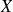suit la loi de Laplace-Gauss (ou loi normale centrée réduite) si elle admet une densité
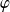telle que :
.
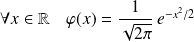On note
.
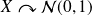Son espérance est
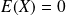et sa variance est
.
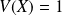La fonction de répartition
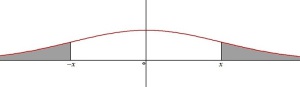
La parité de la densité
|  |
On utilise une table pour obtenir une approximation des valeurs prises par
.
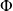Définition :
Une variable aléatoire
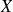suit la loi normale de paramètres
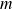et
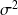si la variable
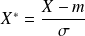suit la loi normale centrée réduite.
Elle admet une densité
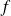telle que :
.
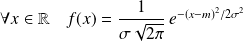On note
.
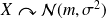Son espérance est
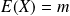et sa variance est
.
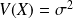Une variable aléatoire
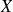suit la loi normale de paramètres
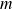et
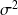si et seulement si sa variable centrée réduite associée suit la loi normale centrée réduite.
