Etude d'un exemple
On se place maintenant dans le cas d'expériences aléatoires pour lesquelles l'univers
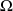 n'est ni un ensemble fini, ni un ensemble infini dénombrable, mais par exemple un intervalle de
n'est ni un ensemble fini, ni un ensemble infini dénombrable, mais par exemple un intervalle de
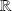 .
.
Exemple :
Un cycliste roule avec une vitesse uniforme sur une piste circulaire. Lorsque vous arrivez, la compétition est déjà commencée.
Quelle est la probabilité qu'à l'instant où vous arrivez le cycliste passe la ligne de départ ?
On a une expérience aléatoire. On peut repérer la position
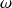 du cycliste par exemple par l'angle
du cycliste par exemple par l'angle
 que fait cette position avec la ligne de départ.
que fait cette position avec la ligne de départ.
On définit ainsi une application
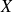 de
de
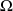 dans
dans
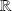 telle que
telle que
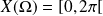 .
.
C'est une variable aléatoire et on cherche à déterminer
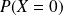 .
.
A priori, on ne sait pas déterminer cette probabilité. Cependant, n'ayant pas d'information sur la vitesse, l'heure,... on peut dire que la probabilité est uniforme, c'est-à-dire que le cycliste a la même probabilité de se trouver n'importe où sur la piste.
On est sûr qu'il est sur la piste :
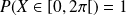 .
.
Il a autant de chances de se trouver sur la première moitié de la piste que sur la seconde :
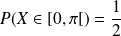 .
.
Et plus généralement, si
 est un entier naturel non nul :
est un entier naturel non nul :
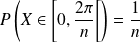 .
.
Cela montre en faisant tendre
 vers
vers
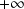 que
que
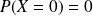 .
.
Et ce serait vrai partout, alors que, cependant
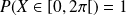 .
.
Ce n'est donc pas en calculant
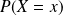 , que l'on aura des renseignements sur la variable aléatoire.
, que l'on aura des renseignements sur la variable aléatoire.
En réalité, la vitesse étant uniforme, ce que l'on sait évaluer, c'est la probabilité que la position du cycliste soit comprise entre deux valeurs
 et
et
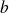 (
(
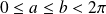 ), car il y a proportionnalité entre cette probabilité et l'angle
), car il y a proportionnalité entre cette probabilité et l'angle
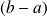 de la portion de piste considérée :
de la portion de piste considérée :
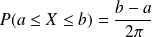 .
.
Or on a vu avec les variables discrètes que
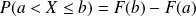 si
si
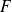 est la fonction de répartition de
est la fonction de répartition de
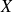 :
:
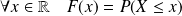 .
.
C'est donc la fonction de répartition qui va nous permettre de connaître les variables aléatoires sur les ensembles non dénombrables.
Ici
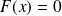 si
si
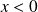 ,
,
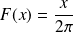 si
si
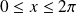 et
et
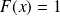 si
si
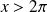 .
.
On peut remarquer que
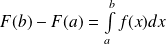 avec
avec
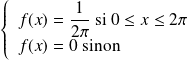 .
.
La fonction
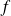 est appelée densité de probabilité de
est appelée densité de probabilité de
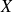 .
.
Dans notre cas, c'est une fonction constante sur
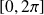 et nulle ailleurs : on dira ici que
et nulle ailleurs : on dira ici que
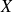 suit la loi uniforme sur l'intervalle
suit la loi uniforme sur l'intervalle
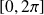 .
.
De telles variables aléatoires sont appelées variables à densité.





