Exemple
Exemple :
Soit
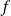 la fonction définie par :
la fonction définie par :
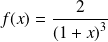 si
si
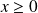 et
et
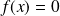 sinon.
sinon.
Montrer que la fonction
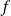 est une densité de probabilité.
est une densité de probabilité.
Il est évident que :
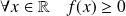 .
.La fonction
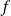 est continue sur
est continue sur
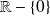 .
.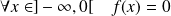 , donc
, donc
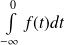 est convergente et
est convergente et
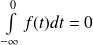 .
.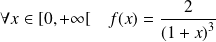 , donc :
, donc :
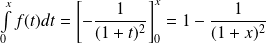 .
.Donc
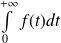 est convergente et
est convergente et
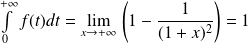 .
.Donc
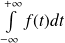 est convergente et
est convergente et
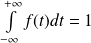 .
.
Conclusion : La fonction
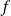 est une densité de probabilité.
est une densité de probabilité.
