Lévitation électromagnétique
Consacrer 30 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Un long solénoïde vertical (semi - infini) à section circulaire (de rayon a et possédant n spires jointives par unité de longueur) est parcouru par un courant d'intensité :
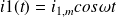
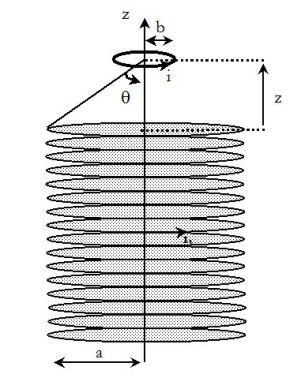
Une bobine circulaire constituée de N spires de rayon b << a, de résistance R, d'inductance L et de masse m, est placée au-dessus du solénoïde à une distance z de son extrémité.
On repère la position de la bobine par l'angle θ.
Question
Calculer le champ magnétique dû au solénoïde au centre de la spire.
Le champ magnétique créé par le solénoïde au niveau de la spire est :
Avec :
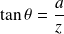
Question
Déterminer l'équation électrique vérifiée par le courant induit
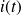dans la bobine. On posera
.
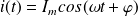On calcule le flux à travers la bobine de ce champ en supposant qu'il est uniforme sur la surface de la spire :
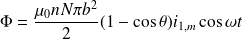
On peut définir le coefficient de mutuelle induction entre la spire et le solénoïde :
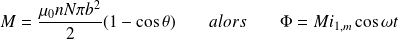
L'équation électrique de la bobine est alors :
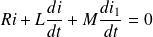
On se place en régime sinusoïdal forcé :
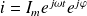
Alors :
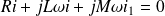
Soit :
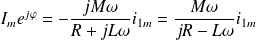
On en déduit :
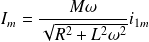
Et :
Question
Montrer que le champ magnétique radial au niveau de la spire peut s'écrire :
On calcule la coordonnée radiale du champ.
Le champ magnétique en dehors de l'axe est obtenu à partir de la conservation du flux magnétique : on prend pour cela un petit cylindre centré sur l'axe Oz, de hauteur dz et de rayon r faible.
Le flux sortant à travers cette surface fermée doit être nulle :
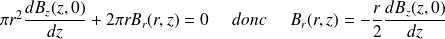
Question
En déduire la force de Laplace qui agit sur la spire. A quelle condition la lévitation est-elle possible ?
L'équilibre éventuel obtenu est-il stable ou instable ?
La force de Laplace (globalement verticale) est alors :
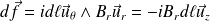
Soit :
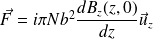
Or :
Et :
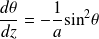(Utiliser
)
D'où :
La force devient :
Soit :
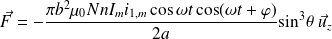
En valeur moyenne : (
)
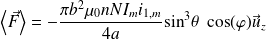
Avec :
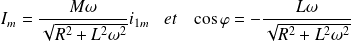
Il vient :
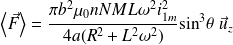
C'est bien une force répulsive (dirigée vers le haut).
Juste au-dessus du solénoïde,
. La lévitation est possible si la force de répulsion est supérieure au poids :
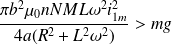
C'est un équilibre stable : si la masse monte, la force de répulsion diminue et la masse retombera.
Idem si elle commence par descendre.
