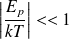Distribution de Maxwell - Boltzmann, assemblée de dipôles
Consacrer 20 minutes de préparation à cet exercice.
Cet exercice n'est pas corrigé. Alors, n'hésitez pas à proposer votre solution sur le forum et à poser des questions si vous ne parvenez pas à trouver une solution.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
On considère deux dipôles permanents, dont les moments
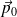et
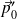(de normes éventuellement différentes) sont portés sur un même axe de vecteur unitaire
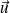, sont à la distance r l'un de l'autre.
On se place dans l'hypothèse où il n'y a que deux orientations possibles :
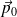et
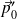peuvent être soit parallèles soit anti-parallèles.
Question
Calculer, dans chaque cas, la force qui s'exerce entre les dipôles, en fonction de p0, p'0, r et
.
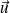On donne, pour ε << 1 :
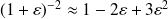
Question
On rappelle que l'énergie potentielle d'un dipôle rigide de moment
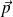, dans un champ électrostatique
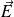est :
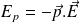
L'agitation thermique est assez forte pour faire passer sans cesse les dipôles de moment
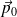et
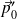d'une position à l'autre.
Calculer la force moyenne qui s'exerce entre les deux dipôles.
On utilisera la répartition de Maxwell - Boltzmann qui donne le nombre de dipôles n(Ep) d'énergie Ep en fonction de la température :
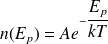
où A est une constante et k la constante de Boltzmann. On supposera que :
