Mouvement d'une barre autour d'un axe fixe
Consacrer 15 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Une barre AB, de longueur 2L et de masse m, est mobile autour d'un axe Az horizontal.
Le point B est fixé à un ressort de constante de raideur k et de longueur à vide
.
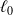L'autre extrémité du ressort est fixe. Dans sa position d'équilibre, la barre est horizontale et le ressort vertical.
La barre est écartée légèrement de sa position d'équilibre puis lâchée sans vitesse initiale.
Question
Déterminer la période des petites oscillations de la barre. On considère que le point B se déplace verticalement.
On utilisera le théorème du moment cinétique puis une méthode énergétique.
On utilise le théorème du moment cinétique par rapport à l'axe (Az), dans le référentiel galiléen du laboratoire. Ce théorème donne :
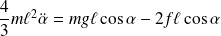
L'angle α étant petit,
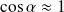. Lorsque la barre est à l'équilibre :
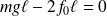
où f0 est la tension du ressort à l'équilibre, qui vaut par ailleurs :
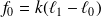
où
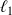est la longueur du ressort à l'équilibre.
Quand la barre fait l'angle α, la longueur du ressort a varié de
et f vaut :
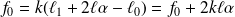
L'équation du mouvement devient alors :
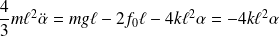
Soit :
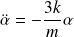
La barre effectue donc des oscillations sinusoïdales de période :
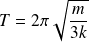
Méthode énergétique :
L'énergie cinétique de la barre est :
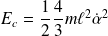
L'énergie potentielle, somme de celle du poids et du ressort est :
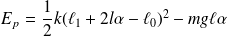
L'énergie mécanique se conserve :
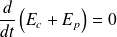
Soit :
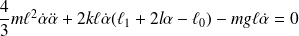
En utilisant la condition d'équilibre, on retrouve l'équation différentielle précédente.
