Décharge d'une sphère chargée
Consacrer 20 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Soit une sphère chargée de charge Q(t), de rayon R et M un point a une distance r>R du centre, placée dans un fluide de conductivité
.
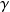Le but de cet exercice sera d'étudier la décharge de cette sphère dans le fluide.
Question
Démontrer que le champ électrique
ne dépend que de r et de t et que le champ magnétique
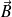est nul.
Penser aux symétries et aux invariances.
Tout plan contenant la droite OM est plan de symétrie pour la répartition de charges, par conséquent :
On raisonne en coordonnées sphériques pour le champ magnétique : par raison de symétrie, le champ magnétique doit être à la fois porté par
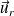et
: il est donc nul.
Question
Calculer
et en déduire
.
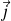Question
A l aide d'une équation de Maxwell, déterminer une équation différentielle en Q(t).
La résoudre et donner le temps caractéristique de décharge.
On utilise l'équation de Maxwell-Ampère, avec un champ magnétique nul :
Avec :
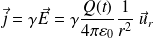
Il vient :
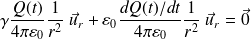
Ainsi :
Autre méthode :
Par définition de l'intensité :
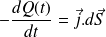
D'où :
Soit :
Dont la résolution est :
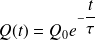
Avec le temps caractéristique de décharge :
Question
Retrouver cette équation et le temps caractéristique en utilisant un bilan d'énergie électromagnétique.
Un bilan d'énergie donne, au niveau local :
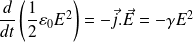
Soit :
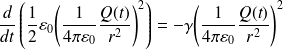
D'où :
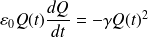
On retrouve ainsi l'équation précédente :
