Exo 10
Question
Montrer que, pour tout entier naturel
 , il existe un unique polynôme
, il existe un unique polynôme
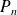 tel que :
tel que :
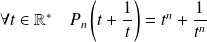 .
.
Commencez par justifier l'unicité.
Raisonnez par récurrence pour prouver l'existence.
La fonction
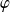 :
:
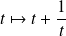 est définie, impaire et de classe
est définie, impaire et de classe
 sur
sur
 et
et
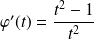 .
.
Donc
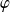 est continue et décroissante sur
est continue et décroissante sur
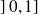 , puis croissante sur
, puis croissante sur
 .
.
De plus
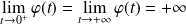 . Donc :
. Donc :
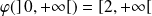 et
et
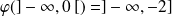 .
.
On peut déjà remarquer qu'il y a unicité car si deux polynômes convenaient, ils coïncideraient pour tout
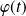 , donc au moins sur
, donc au moins sur
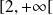 , donc ils seraient égaux.
, donc ils seraient égaux.
Pour montrer l'existence, on raisonne par récurrence double.
Initialisation :
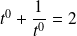 , donc :
, donc :
 en posant
en posant
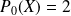 .
.
Et :
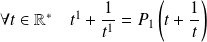 en posant
en posant
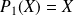 .
.
Donc
 et
et
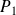 existent.
existent.
Hérédité : Soit
 tel que
tel que
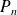 et
et
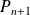 existent.
existent.
Donc :
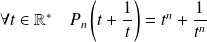 et
et
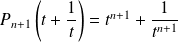 .
.
Or :
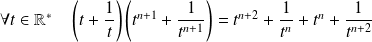 .
.
Donc :
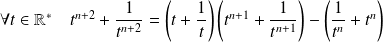 .
.
Donc :
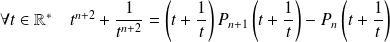 .
.
Donc :
 en posant :
en posant :
 .
.
Donc
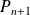 et
et
 existent.
existent.
Conclusion :
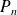 et
et
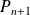 existent pour tout
existent pour tout
 .
.
Conclusion : Pour tout entier
 , il existe un unique polynôme
, il existe un unique polynôme
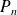 tel que
tel que
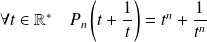 .
.
Question
Déterminer le degré de
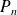 , son coefficient dominant et sa parité.
, son coefficient dominant et sa parité.
A l'aide des premiers termes, conjecturez un résultat puis démontrez le par récurrence.
On a :
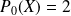 ,
,
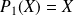 et
et
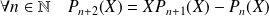 .
.
Donc :
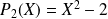 ,
,
 et
et
 .
.
On conjecture donc que
 , que son coefficient dominant est
, que son coefficient dominant est
 si
si
 et que
et que
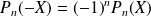 . Notons
. Notons
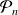 cet ensemble de propriétés.
cet ensemble de propriétés.
Pour montrer que
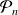 est vraie pour tout
est vraie pour tout
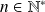 , on raisonne par récurrence double.
, on raisonne par récurrence double.
Initialisation : D'après les calculs précédents,
 et
et
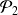 sont vraies.
sont vraies.
Hérédité : Soit
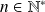 tel que
tel que
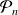 et
et
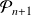 soient vraies.
soient vraies.
 . Or :
. Or :
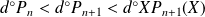 .
.
Donc :
 d'après l'hypothèse de récurrence.
d'après l'hypothèse de récurrence.
Et le coefficient dominant de
 est celui de
est celui de
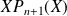 , donc d'après l'hypothèse de récurrence, ce coefficient est
, donc d'après l'hypothèse de récurrence, ce coefficient est
 .
.
 . Donc d'après l'hypothèse de récurrence :
. Donc d'après l'hypothèse de récurrence :
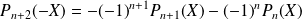 .
.
Or :
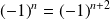 . Donc :
. Donc :
 .
.
Conclusion :
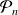 et
et
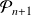 sont vraies pour tout
sont vraies pour tout
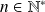 .
.
Conclusion : Pour tout
 ,
,
 , le coefficient dominant de
, le coefficient dominant de
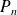 est
est
 si
si
 et
et
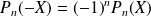 (donc
(donc
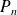 est de même parité que
est de même parité que
 ).
).
Question
Déterminer les racines du polynôme
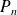 .
.
Déterminez d'abord le nombre maximal de racines, puis utilisez la définition de
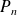 pour les déterminer.
pour les déterminer.
 , donc
, donc
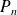 a au plus
a au plus
 racines distinctes. Or :
racines distinctes. Or :
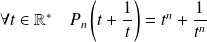 .
.
Donc si
 , alors
, alors
 est une racine de
est une racine de
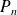 .
.
Or
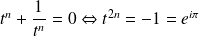 . Donc :
. Donc :
 .
.
Donc si
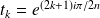 , une racine de
, une racine de
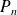 est :
est :
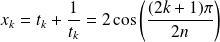 .
.
Et
 .
.
Donc
 ,
,
 , ...,
, ...,
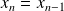 . Il reste
. Il reste
 racines distinctes
racines distinctes
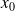 ,
,
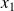 , ...,
, ...,
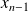 .
.
Conclusion :
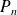 admet
admet
 racines distinctes :
racines distinctes :
 pour
pour
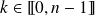 .
.





