Exo 9
Question
Déterminer les polynômes
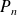 définis par
définis par
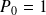 ,
,
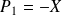 et
et
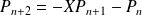 .
.
Pensez à la récurrence linéaire d'ordre
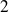 .
.
Fixons
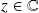 , et posons :
, et posons :
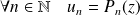 . Donc :
. Donc :
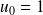 et
et
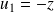 .
.
La suite
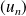 suit une récurrence linéaire d'ordre
suit une récurrence linéaire d'ordre
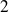 :
:
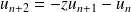 .
.
L'équation caractéristique est :
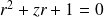 . Le discriminant est :
. Le discriminant est :
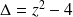 .
.
Soit
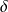 une racine carrée de
une racine carrée de
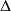 . Donc :
. Donc :
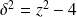 et
et
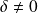 si
si
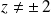 .
.
Si
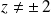 , l'équation admet deux racines distinctes
, l'équation admet deux racines distinctes
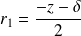 et
et
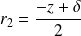 .
.
Et il existe deux complexes
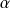 et
et
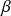 tels que :
tels que :
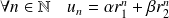 .
.
Donc :
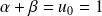 et
et
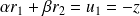 . Donc :
. Donc :
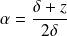 et
et
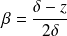 .
.
Donc :
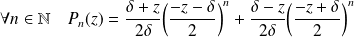 .
.
Donc :
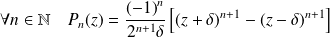 .
.
Or :
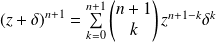 et
et
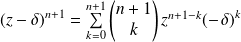 .
.
Donc :
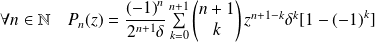 .
.
Lorsque
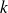 est pair, le terme est nul, donc il ne reste que les termes où
est pair, le terme est nul, donc il ne reste que les termes où
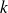 est impair.
est impair.
Donc en posant
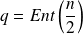 :
:
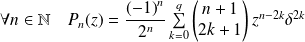 .
.
Or :
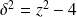 . Donc :
. Donc :
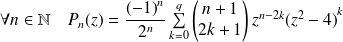 .
.
Donc
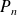 coïncide avec le polynôme
coïncide avec le polynôme
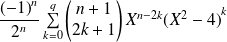 sur
sur
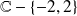 .
.
Deux polynômes qui coïncident sur une infinité de valeurs sont égaux.
Conclusion :
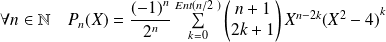
On peut préciser ses coefficients.
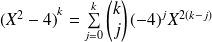 . Donc :
. Donc :
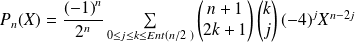 .
.
Donc :
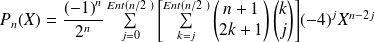 .
.
Question
Calculer les racines de
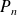 .
.
Utilisez les racines de l'unité.
On peut remarquer que
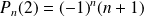 et
et
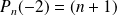 .
.
Donc
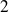 et
et
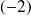 ne sont pas racines de
ne sont pas racines de
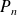 . Donc, si
. Donc, si
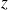 est une racine de
est une racine de
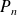 , alors
, alors
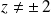 .
.
Donc :
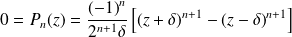 . Donc :
. Donc :
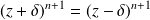 .
.
Or
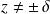 car
car
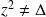 . Donc :
. Donc :
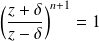 . Donc :
. Donc :
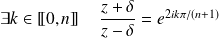 .
.
Or :
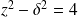 . Donc :
. Donc :
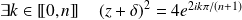 et
et
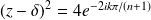 .
.
Donc en additionnant :
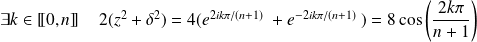 .
.
Donc :
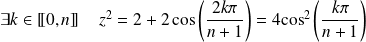 , donc
, donc
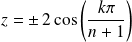 .
.
De plus
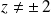 , donc
, donc
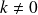 . Donc :
. Donc :
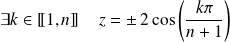 .
.
Et on peut remarquer que, si
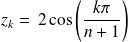 , alors
, alors
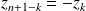 . Donc les racines sont comptées
. Donc les racines sont comptées
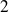 fois, ce qui est logique puisque un polynôme de degré
fois, ce qui est logique puisque un polynôme de degré
 a
a
 racines.
racines.
Conclusion : Les racines de
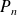 sont les complexes
sont les complexes
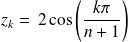 où
où
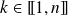 .
.





