Exo 6
Question
Déterminer dans
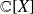les polynômes
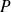tels que :
.
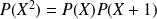Commencez par chercher quels sont les polynômes constants qui sont solutions.
Déterminez ensuite les racines des autres polynômes et déduisez en leur factorisation.
Les polynômes constants
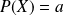sont solutions si et seulement si :
.
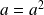Donc il n'y a que deux polynômes constants solutions :
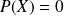et
.
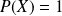Soit
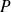un polynôme solution non constant. Donc il admet au moins une racine
.
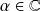Donc
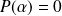, donc
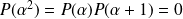. Donc
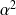est aussi racine de
.
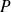Une récurrence évidente montre que, pour tout
,
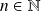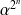est racine de
.
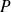Or
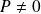, donc
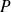ne peut pas avoir une infinité de racines. Donc il existe au moins deux entiers
et
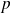distincts tels que
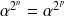, donc
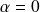ou
.
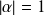De plus, si
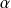est racine de
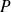, alors :
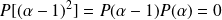, donc
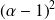est racine de
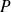et le même raisonnement conduit à
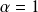ou
.
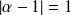Donc, si
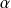est racine de
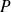, alors :
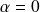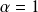ou
ou
.
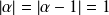Or
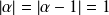équivaut à
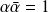et
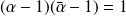, donc à
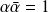et
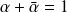, donc à
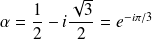ou
.
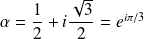Donc les seules racines possibles de
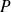sont
,
,
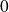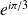et
.
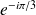Donc le polynôme
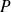est de la forme :
.
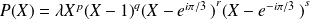Donc :
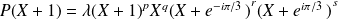car
.
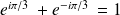Et :
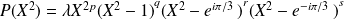. Or :
.
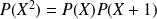Si
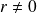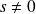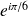et
,
et
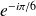sont racines de
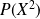. Or
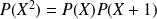, mais
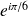et
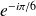ne sont racines ni de
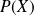, ni de
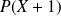. Donc :
.
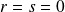Donc :
.
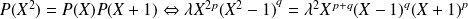Donc :
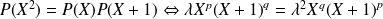. Donc
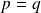et
.
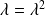Donc :
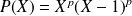car
.
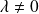Conclusion : Les polynômes
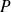tels que
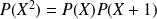sont
,
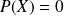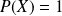et les polynômes de la forme
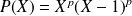où
.
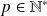