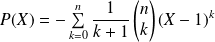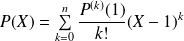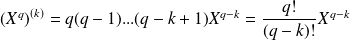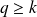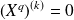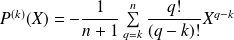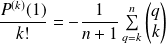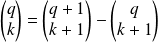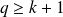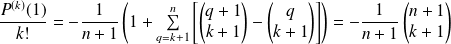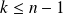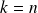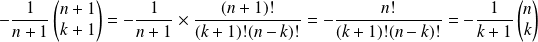Exo 7
Question
Soit
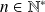 . Montrer qu'il existe un unique polynôme
. Montrer qu'il existe un unique polynôme
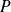 (que l'on déterminera) qui vérifie :
(que l'on déterminera) qui vérifie :
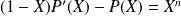 .
.
Indice
Commencez par déterminer le degré du polynôme, puis déterminez ses coefficients.
Solution
Remarquons d'abord que le polynôme nul n'est pas solution.
Soit
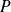 un polynôme solution. Soit
un polynôme solution. Soit
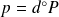 .
.
Donc :
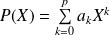 avec
avec
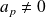 . Et :
. Et :
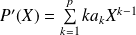 .
.
Donc :
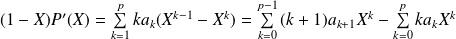 .
.
Donc :
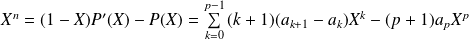 .
.
Par unicité du degré :
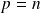 .
.
Par unicité des coefficients :
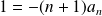 et
et
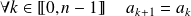 .
.
Donc :
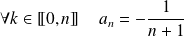 .
.
Conclusion : L'équation a une unique solution
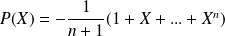 .
.