Exo 3
Question
Résoudre suivant les valeurs du réel
le système :
.
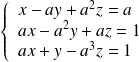Commencez par étudier la dépendance linéaire des vecteurs
,
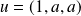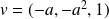et
.
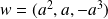Soient les vecteurs
,
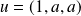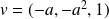et
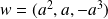de
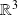. Le système équivaut à :
.
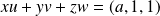Donc le problème revient à exprimer le vecteur
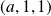comme combinaison linéaire de
,
et
.
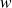Etudions la dépendance linéaire des vecteurs
,
et
.
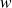Le déterminant des trois vecteurs (donc du système) est :
.
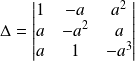Par la transformation
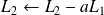et
:
.
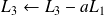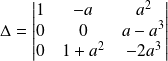Donc :
.
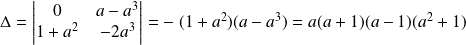Si
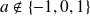, alors
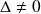, donc les trois vecteurs forment une base de
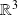et donc le système admet une unique solution.Par substitution :
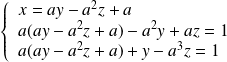, donc
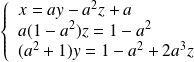, donc
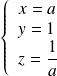.Donc, si
:
.
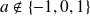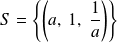Si
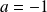, le système devient :
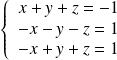, donc
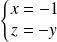.Donc, si
:
.
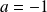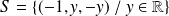Si
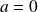, la deuxième ligne du système est :
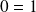.Donc, si
:
.
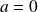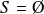Si
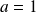, le système devient :
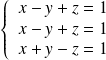, donc
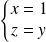.Donc, si
:
.
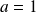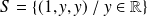Conclusion :
Si
:
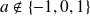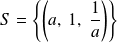.Si
:
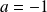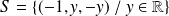.Si
:
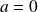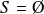.Si
:
.
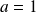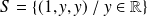