Exo 2
On considère la matrice
.
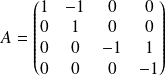Question
Calculer
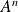pour tout entier
.
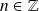Pour les puissances positives, décomposez la matrice
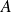en somme de deux matrices qui commutent et dont les puissances sont faciles à calculer, et utilisez la formule du binôme.
Inversez ensuite la matrice.
On peut remarquer que
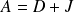en posant :
, et :
.
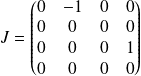Or :
.
Et :
.
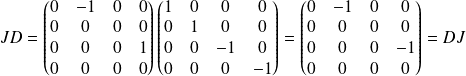Donc les matrices
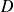et
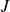commutent.
Donc, d'après la formule du binôme :
.
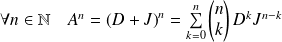Or
.
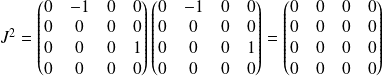Donc :
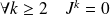. Donc :
.
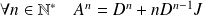Donc :
.
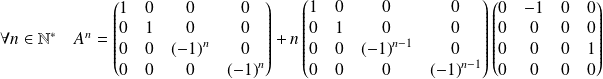Donc :
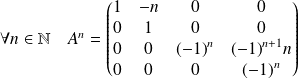car cette expression est encore valable si
.
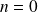Cette matrice est inversible car elle est triangulaire sans zéros sur la diagonale. On l'inverse en résolvant un système.
L'équation matricielle
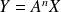équivaut au système :
.
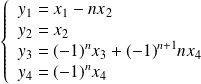Donc l'équation matricielle
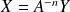équivaut au système :
.
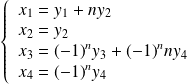Donc :
.
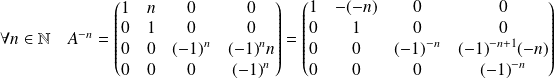Conclusion :
.
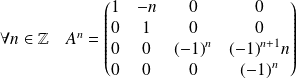Autre solution
On remarque que :
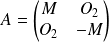, avec :
.
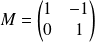Donc :
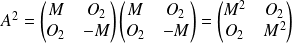, avec :
.
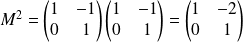Et :
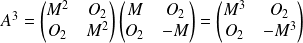, avec :
.
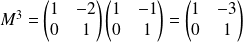Une récurrence évidente montre que :
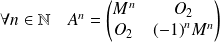, avec :
.
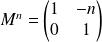La matrice
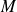est inversible et :
.
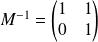Or :
.
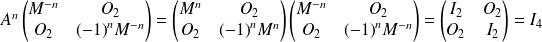Donc
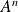est inversible et :
.
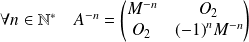Et
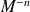est l'inverse de
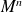, donc
.
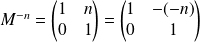Donc :
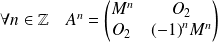, avec :
.
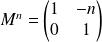Conclusion :
.
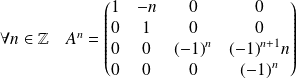