Espérance mathématique et variance
On considère un espace probabilisé
.
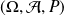Définition :
Soit
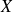une variable aléatoire discrète d'univers image
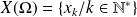. On pose :
.
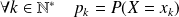Si la série de terme général
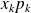est absolument convergente, on appelle espérance mathématique de
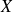le réel
.
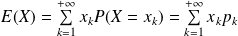Contrairement aux variables discrètes finies, certaines variables aléatoires discrètes infinies n'ont pas d'espérance mathématique. Il faut étudier la convergence de la série de terme général
.
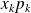On reprend l'exemple précédent.
Exemple :
Exemple
On a vu que la loi de probabilité de
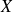est définie par :
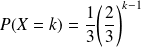pour tout
.
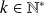La variable aléatoire
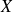a-t-elle une espérance ?
Les propriétés des espérances des variables discrètes finies s'étendent aux variables discrètes infinies sous réserve d'existence.
Fondamental :
Propriétés
Si
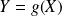, alors :
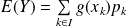sous réserve de convergence absolue (Théorème de transfert).
.
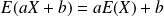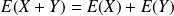si
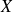et
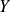sont deux variables aléatoires discrètes infinies ayant une espérance.
Comme pour les variables aléatoires discrètes finies, la variable est centrée si
.
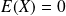Comme pour les variables aléatoires discrètes finies, on appelle moment d'ordre r de
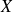l'espérance de la variable
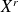, sous réserve d'existence.
Définition :
Si
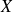est une variable aléatoire discrète infinie qui possède une espérance, on appelle variance de
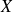le moment d'ordre
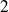de la variable aléatoire centrée associée à
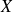, c'est-à-dire le réel :
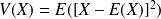sous réserve d'existence.
Son écart-type est le réel :
.
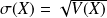Certaines variables aléatoires discrètes infinies n'auront donc pas de variance.
Les propriétés des variances des variables discrètes finies s'étendent aux variables discrètes infinies sous réserve d'existence.
Fondamental :
Propriétés
.
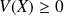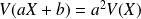pour tous réels
et
.
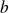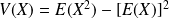(Théorème de Koenig-Huygens).
.
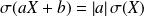On reprend l'exemple précédent.
Exemple :
Exemple
On a vu que la loi de probabilité de
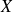est définie par :
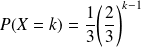pour tout
.
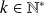L'espérance de
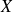est :
.
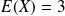La variable aléatoire
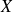a-t-elle une variance ?
Comme pour les variables aléatoires discrètes finies, la variable est centrée réduite si
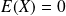et
.
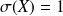La variable centrée réduite associée à
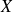est
.
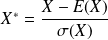L'inégalité de Bienaymé-Tchebychev reste valable.
Fondamental :
Inégalité de Bienaymé-Tchebychev
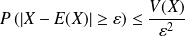pour tout
.
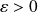