Variable aléatoire discrète infinie
Dans tout ce qui suit, on considère un espace probabilisé
.
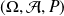Définition :
Une variable aléatoire réelle
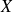sur
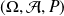est discrète infinie si son univers image
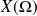est un ensemble infini dénombrable.
Les éléments de
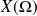peuvent donc être numérotés sur
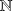ou
.
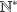Les définitions sont analogues à celles des variables discrètes finies, mais se posent des problèmes de convergence.
Définition :
Soit
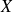une variable aléatoire discrète d'univers image
.
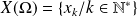La loi de probabilité de
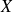est l'ensemble des réels
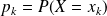pour tout
.
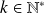Propriété :
.
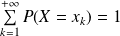Il s'agit cette fois de la somme d'une série convergente.
On reprend l'exemple déjà cité.
Exemple :
Exemple : Dans une urne qui contient
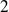boules blanches et
boule rouge, on fait des tirages successifs avec remise d'une boule et
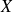est le rang de la première boule rouge tirée.
Déterminer la loi de probabilité de la variable aléatoire
.
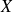Les notations des événements sont les mêmes que pour les variables discrètes finies.
Définition :
La fonction de répartition de la variable aléatoire
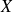est la fonction définie par :
.
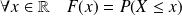Propriétés :
La fonction de répartition est une fonction en escalier croissante.
Elle est continue à droite en tout réel
.Elle admet pour limites :
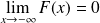et
.
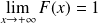Méthode :
Détermination pratique :
On suppose que l'univers image est
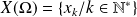avec
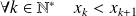et
.
.
.
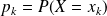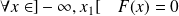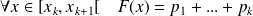Les opérations sur les variables aléatoires discrètes infinies sont les mêmes que pour les variables discrètes finies :
Somme
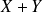de deux variables aléatoires discrètes finies ou infinies.Produit
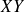de deux variables aléatoires discrètes finies ou infinies.Image
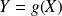d'une variable aléatoire discrète finie ou infinie
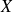par une fonction
.
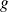