Lois usuelles discrètes infinies
Comme pour les variables discrètes finies, il s'agit de repérer quelques situations "modèles".
On se place toujours dans un espace probabilisé
.
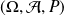La première loi usuelle est celle de l'exemple étudié précédemment.
Définition :
Une variable aléatoire
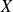suit la loi géométrique de paramètre
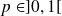si :
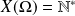et
.
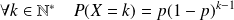On note :
.
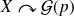Son espérance est
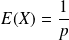et sa variance
.
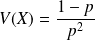Si l'on répète dans les mêmes conditions et de manière indépendante une épreuve de Bernoulli dont la probabilité de succès est
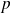, le rang
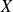du premier succès suit la loi géométrique
.
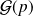Dans l'exemple précédent, l'urne contient
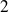boules blanches et
boule rouge, donc la probabilité de tirer une boule rouge (succès) est
.
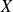est le rang de la première boule rouge tirée, donc du premier succès. Donc
.
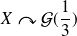Remarque :
Cette définition pose le problème de l'existence d'un succès et n'évoque pas le cas où il n'y a jamais de succès.
En effet :
.
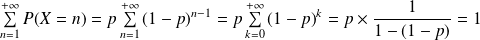Donc, on est quasiment sûr d'avoir au moins un succès.
La deuxième loi infinie usuelle est une "loi limite" comme on le verra un peu plus tard.
Elle modélise les flux d'individus pendant une période donnée : clients à un guichet, péage d'autoroute, ...
Définition :
Une variable aléatoire
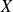suit la loi de Poisson de paramètre
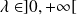si :
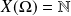et
.
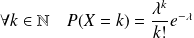On note :
.
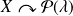Son espérance est
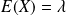et sa variance
.
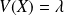