Solution

La loi de la variable aléatoire est  définie par : 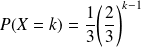pour tout 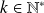et son espérance est : .

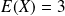Pour faciliter les calculs, on calcule l'espérance de la variable aléatoire .

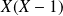D'après le théorème de transfert : 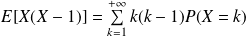sous réserve de convergence.

Or : .

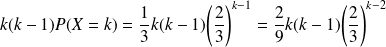La série de terme général 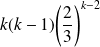est une série dérivée d'une série géométrique.

Elle converge car : 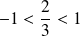. Donc la série de terme général 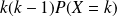est absolument convergente.

Donc la variable aléatoire 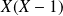a une espérance mathématique.

Donc : .

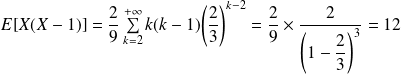Or par linéarité : 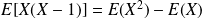. Donc : .

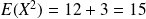Et : .

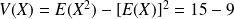Conclusion : La variance de 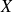est .
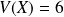