Théorie cinétique du gaz parfait
Conseil : Pour commencer la thermo, une image pour se motiver ...
Fondamental : Le modèle du gaz parfait macroscopique
A l'échelle macroscopique : un gaz parfait est un gaz (réel !) étudié à faibles pressions (inférieures à quelques bars, 1 bar = la pression atmosphérique normale).
Un gaz est caractérisé par des paramètres macroscopiques mesurables à notre échelle : volume V, pression P, température T (en Kelvin) ou t (en °C) et la quantité de matière n.
Ces paramètres sont appelés « variables d'état ».
Ces variables sont définies à « l'équilibre thermodynamique » du gaz.
Relation entre T (échelle Kelvin) et t (échelle Celsius) :
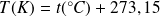
Dans le SI, l'unité de pression est le Pascal.
On utilise aussi le bar :
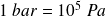
L'équation d'état d'un gaz parfait est :
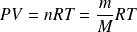
où
est le nombre de moles,
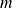la masse de gaz et
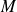sa masse molaire.
Fondamental : Le modèle du gaz parfait microscopique
On considère un gaz monoatomique (Ar, He, H, ...) à la température T, la pression P et occupant un volume V.
On note :
n : nombre de moles
N : nombre total de particules dans le volume V
n* : densité particulaire (nombre de particules par unité de volume) :
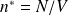
Hypothèses du modèle :
Les particules ont un mouvement incessant (agitation thermique)
Les particules n'interagissent pas entre elles mais seulement avec la paroi lors de chocs avec celle-ci. Elles sont ponctuelles.
Les vitesses des particules sont distribuées selon une loi statistique appelée loi de distribution de Maxwell – Boltzmann.
La distribution des vitesses des particules est homogène (indépendante du point où l'on se place) et isotrope (indépendante de la direction choisie).
La densité particulaire est la même en tout point du récipient (répartition homogène des particules)
Fondamental : Calcul de la pression cinétique
Dans la suite, on choisit un modèle simple (simpliste !) de loi de répartition des vitesses moléculaires :
Les particules (de masse m) ont toutes la même vitesse (en norme), notée v.
Les particules ne peuvent se diriger que dans trois directions (Ox, Oy et Oz) et donc six sens.
La pression cinétique P résulte des chocs incessants des particules contre la paroi.
A l'échelle particulaire, ces chocs sont élastiques (conservations de la quantité de mouvement et de l'énergie cinétique).
La quantité de mouvement acquise par la paroi lors d'un choc est (conservation de la quantité de mouvement) :
Pendant l'intervalle de temps dt, la force subie par la paroi est :
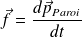
Où
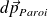est la quantité de mouvement reçue par la paroi lors des chocs de particules tombant sur la paroi pendant dt.
Si dN désigne le nombre de particules qui choquent la paroi pendant l'intervalle de temps dt, alors :
La pression cinétique P s'en déduit :
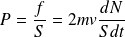
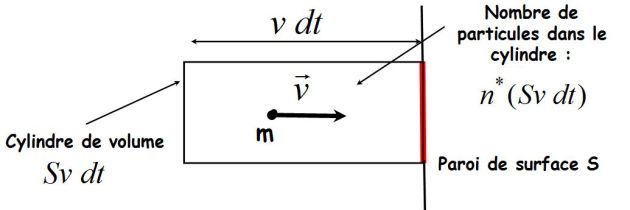
Calcul de dN : (voir figure suivante)
Les particules ont « une chance sur six » de se diriger vers la paroi.
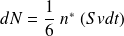
On en déduit la pression cinétique P :
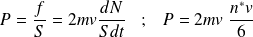
Soit :
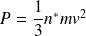
Un calcul plus réaliste, prenant en compte la distribution de Maxwell-Boltzmann conduit à un résultat comparable, à condition de remplacer v par la vitesse quadratique u :
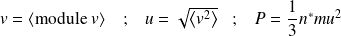
Complément : Une vidéo sur la pression cinétique
Une vidéo sur le calcul de la pression cinétique pour un gaz parfait monoatomique
Fondamental : Lien avec le modèle macroscopique du gaz parfait
Sachant que :
Il vient :
Cette équation est à comparer à l'équation d'état macroscopique d'un GP :
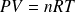
Or :
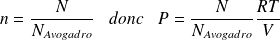
D'où :
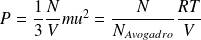
On en déduit ainsi l'expression de la vitesse quadratique u en fonction de la température absolue T :
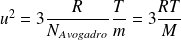
où
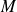est la masse molaire.
On note :
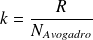
la constante de Boltzmann (
).
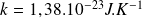Finalement :
Quelques applications numériques :
A 300 K, pour l'hélium,
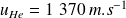et pour l'Argon,
.
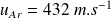Fondamental : Interprétation cinétique de la température
L'énergie cinétique moyenne d'une particule, notée <ec>, s'exprime en fonction de la température T :
La température est une mesure de l'agitation thermique des particules.
Il est commode, parfois, d'exprimer une température T en eV, keV ou encore MeV (qui sont des unités énergétiques) : la correspondance entre T en eV et T en K s'obtient à partir de la relation précédente.
Ainsi, si T vaut 100 eV, alors, en K :
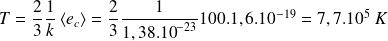
Fondamental : L'énergie interne d'un gaz parfait monoatomique
Puisque l'on néglige les forces d'interaction mutuelle entre particules, l'énergie potentielle d'interaction mutuelle (définie en mécanique, dans le cas de deux corps en interaction) est nulle.
Dans le référentiel du laboratoire (dans lequel le récipient contenant le gaz est supposé immobile), l'énergie mécanique du système de N particules est appelée « Energie interne » et notée U.
Elle vaut :
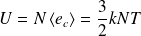
Elle représente l'énergie contenue à l'intérieur du récipient, due à l'agitation thermique (d'où le nom d'énergie interne).
Avec :
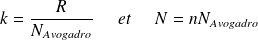
Il vient :
Ainsi :
Complément : Cas d'un gaz parfait diatomique
Nous admettrons que, pour un gaz parfait diatomique, l'équation d'état est identique à celle d'un gaz parfait monoatomique.
Par contre, la molécule pouvant osciller autour de sa position moyenne d'équilibre, l'énergie interne contient des termes supplémentaires.
Deux « degrés de libertés » supplémentaires apparaissent et l'énergie interne vaut (aux températures usuelles que l'on considère) :
Complément : L'équation d'état de Van der Waals
Van der Waals (physicien hollandais, 1837 – 1923) a proposé une équation d'état qui prend en compte à la fois le volume des particules et l'existence de forces intermoléculaires en moyenne attractives (à longue distance).
C'est une équation d'état phénoménologique (basée sur l'expérience), qui s'écrit (pour une mole de gaz) :
a et b sont des constantes caractéristiques du gaz.
Pour n moles, on a :
On retrouve, dans le cas où on néglige les termes correctifs, l'équation des gaz parfaits,
.
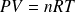Le volume réellement accessible aux molécules est de l'ordre de V – b, où b (appelé covolume molaire) correspond au volume qu'occuperaient les molécules si elles étaient entassées (comprimées) les unes contre les autres :
où
est le rayon d'une particule de gaz supposée sphérique (de l'ordre du nm).
