Loi d'Ohm locale
Méthode : Présentation du modèle de Drude (1900)
Dans un conducteur métallique (« ohmique ») soumis à une tension électrique, les électrons de conduction se mettent en mouvement.
On définit l'intensité I du courant électrique et le vecteur
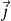densité de courant électrique :
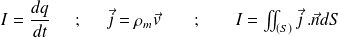
Avec :
: densité de charges mobiles (
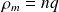, où
est la densité de charges mobiles).
: vitesse des porteurs de charge
Soit
le champ électrique responsable de la mise en mouvement des charges mobiles.
Une charge mobile est d'une part soumise à la force électrique :
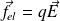
Elle est également soumise à une force due aux charges fixes qui composent le réseau cristallin du conducteur métallique.
On modélise cette force par une force de type « frottement fluide » :
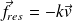
où k est une constante phénoménologique, dépendant du conducteur ohmique considéré.
Fondamental : Loi d'Ohm locale et conductivité d'un conducteur ohmique
Le PFD appliqué (dans le référentiel du laboratoire) à une charge mobile donne alors (m désigne la masse d'un porteur de charge) :
On pose :
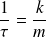
Avec
le temps de relaxation du milieu ohmique.
L'équation différentielle devient :
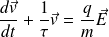
Si l'on suppose le champ électrique constant (indépendant du temps), la solution de cette équation différentielle est :
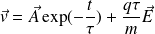
En régime permanent (pour
) :
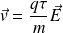
Le vecteur densité de courant s'en déduit :
On pose :
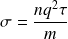
la conductivité électrique du milieu.
Attention : Loi d'Ohm locale
Pour un conductivité ohmique de conductivité
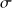(et de résistivité électrique
) :
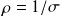La loi d'Ohm locale est ainsi expliquée à partir de la limitation de la vitesse de migration des porteurs du fait de leurs interactions avec le milieu matériel (les cations fixes du réseau métallique).
Ordres de grandeur :
Les porteurs de charge sont des électrons.
Le tableau suivant donne les conductivités de quelques métaux usuels à température ambiante (300 K) :
Métaux | Ag | Cu | Au | Al | Hg |
| 6,21 | 5,88 | 4,55 | 3,65 | 0,10 |
Pour le cuivre, on peut évaluer le temps de relaxation :
Le régime permanent est atteint très rapidement, du moins tant que les durées caractéristiques de variations du champ
sont très supérieures à
.
Ainsi, la loi d'Ohm locale restera valable tant que les fréquences du champ électrique ne seront pas trop élevées (c'est l'ARQS, approximation des régimes quasi-stationnaires).
Complément : Résistance électrique et loi d'Ohm macroscopique
On considère un conducteur ohmique cylindrique de section transverse
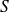et de longueur
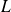(un fil électrique en cuivre, par exemple).
Le champ à l'intérieur du fil est (en régime indépendant du temps) :
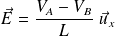
D'après la loi d'Ohm locale :
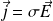
Par ailleurs :
D'où :
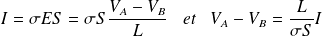
On pose :
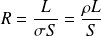
la résistance électrique du fil.
Alors (en convention récepteur) :
