Dipôle électrostatique
Définition : Dipôle électrostatique
On appelle « dipôle électrostatique » un ensemble rigide de deux charges ponctuelles
 et
et
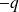 (donc globalement neutre), distantes de
(donc globalement neutre), distantes de
 .
.
Un tel modèle permet d'étudier :
Les molécules polaires (par exemple : HCl, H2O)
La polarisation des atomes dans un champ électrique extérieur (phénomène de solvatation des ions)
Méthode : Détermination du potentiel créé par le dipôle
On calcule le potentiel créé par le dipôle en un point M de l'espace.
Symétrie de révolution autour de l'axe (Oz) : on choisit
 dans le plan des deux charges.
dans le plan des deux charges.
On se place dans le cadre de l'approximation dipolaire :
 (on se place « loin » des charges, c'est-à-dire à des distances bien supérieures à quelques nm).
(on se place « loin » des charges, c'est-à-dire à des distances bien supérieures à quelques nm).

Le potentiel au point M est (principe de superposition) :
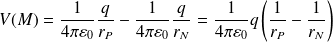
(Avec :
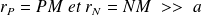 )
)
D'après la relation de Chasles :

En élevant au carré :
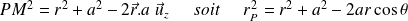
On calcule ensuite
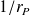 :
:
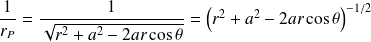
On rappelle le développement limité (à l'ordre 1) de :

On pose
 (x<<1), alors :
(x<<1), alors :
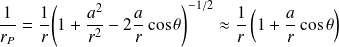
De la même manière (il suffit de remplacer
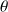 par
par
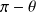 et donc
et donc
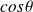 par
par
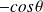 ) :
) :

Ainsi :
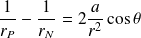
D'où le potentiel :
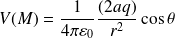
On définit le vecteur moment dipolaire du dipôle électrostatique (vecteur dirigé de la charge négative vers la charge positive) :
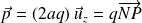
Alors (décroissance du potentiel en
 ) :
) :
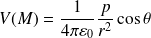
En notant
 :
:

Définition : Vecteur moment dipolaire
Le vecteur moment dipolaire est une caractéristique du dipôle électrostatique.
p s'exprime en C.m dans le SI.
On définit plutôt le Debye, mieux adapté :
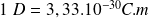
Exemple :
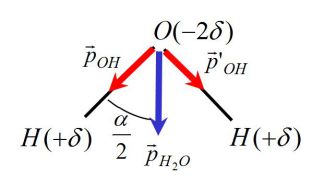
La molécule d'eau a un moment dipolaire .
En déduire les charges
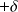 et
et
 portées respectivement par les atomes d'hydrogène et par l'atome d'oxygène.
portées respectivement par les atomes d'hydrogène et par l'atome d'oxygène.
On donne :

Le moment dipolaire total de la molécule est :

Avec :
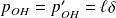
Par conséquent :
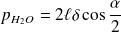
On en déduit :

Méthode : Calcul du champ électrostatique dans le cadre de l'approximation dipolaire
La relation intrinsèque
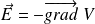 permet de calculer le champ (en coordonnées polaires) :
permet de calculer le champ (en coordonnées polaires) :
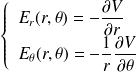
Par conséquent :
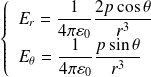
Ou encore :
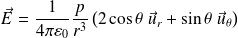
Méthode : Topographie du champ d'un dipôle
Surfaces équipotentielles :
L'équation de la surface équipotentielle (
 ) au potentiel
) au potentiel
 est :
est :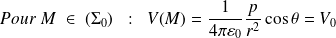
Soit l'équation en coordonnées polaires :

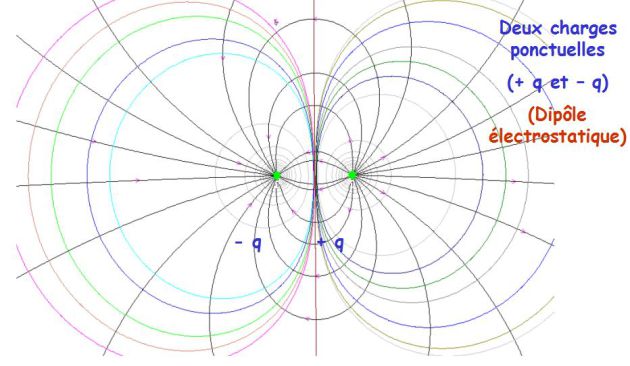
L'allure des lignes équipotentielles est indiquée sur la figure suivante ; l'axe perpendiculaire à (Oz) et passant par O est l'équipotentielle zéro.
Par rotation autour de (Oz), ces lignes engendrent les surfaces équipotentielles.
Lignes de champs :
Sur la ligne de champ passant par M :
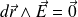
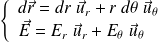
D'où :
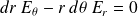
Soit :
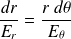

En remplaçant les coordonnées du champ par leurs expressions :
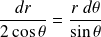
On sépare les variables :

Soit :

On note
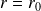 pour
pour
 , alors, en intégrant, on obtient l'équation en coordonnées polaires des lignes de champs (
, alors, en intégrant, on obtient l'équation en coordonnées polaires des lignes de champs (
 est un paramètre) :
est un paramètre) :
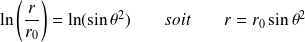
L'allure des lignes de champ est donnée sur la figure précédente.
Fondamental : Action d'un champ électrique extérieur sur un dipôle
On considère un dipôle électrostatique plongé dans un champ électrique
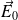 qui peut être supposé uniforme à l'échelle du dipôle.
qui peut être supposé uniforme à l'échelle du dipôle.
Quel est l'effet de ce champ sur le dipôle ?
Système étudié : le dipôle (rigide)
Référentiel d'étude : celui du laboratoire (supposé galiléen)
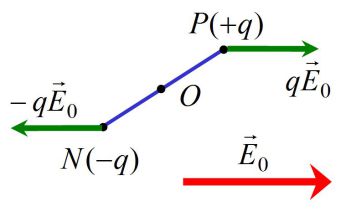
Le dipôle est soumis aux deux forces
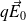 et
et
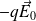 de résultante nulle.
de résultante nulle.
Le dipôle est globalement soumis à un « couple de forces », dont le moment par rapport à O vaut :
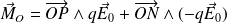
Soit :
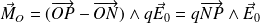
Finalement :

Sous l'effet d'un champ électrique, le dipôle se met à tourner afin de s'aligner selon le sens du champ (
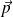 et
et
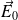 dans le même sens, position d'équilibre stable).
dans le même sens, position d'équilibre stable).
Étude énergétique :
Soit V le potentiel dont dérive le champ
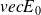 ; l'énergie potentielle du dipôle (rigide) dans ce champ est :
; l'énergie potentielle du dipôle (rigide) dans ce champ est :
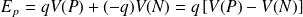
On rappelle que (
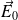 est un champ de gradient) :
est un champ de gradient) :
Par conséquent, avec
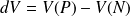 :
:

Et donc :
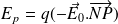
Soit :

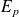 est minimale (position d'équilibre stable) quand
est minimale (position d'équilibre stable) quand
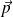 et
et
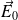 ont même sens.
ont même sens.
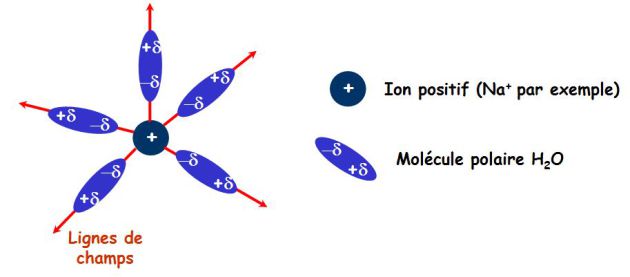
La figure suivante illustre le phénomène de solvatation : les molécules d'eau s'alignent selon les lignes du champ créé par la charge
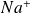 .
.