Étude énergétique des ondes sonores
Méthode : Équation de conservation locale de l'énergie sonore
On fait la somme de l'équation :
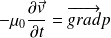
multipliée par va vitesse
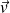et de l'équation :
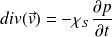
multipliée par la surpression
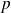. Il vient :
On pose :
La densité volumique d'énergie sonore :
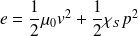
Le premier terme désigne l'énergie cinétique volumique du fluide et le second l'énergie potentielle volumique associée aux forces de pression.
Le vecteur densité surfacique de puissance sonore :
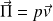
Alors :
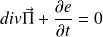
On reconnaît une équation du type "conservation locale d'énergie", déjà vue par exemple pour l'énergie d'un champ électromagnétique ou pour l'équation de conservation de l'énergie dans le cas des phénomènes de conductions thermiques.
Attention : Équation de conservation locale de l'énergie sonore
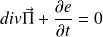
Avec :
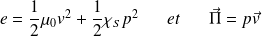
Complément : Cas d'une onde plane progressive
Densités d'énergies :
On considère une OPPH qui se propage dans le sens des
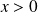. Alors
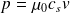. Ainsi :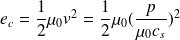 
Or :
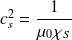
D'où :
Ainsi, pour une OPPH, les densités d'énergies cinétique et potentielle sont égales.
La densité d'énergie totale vaut alors :
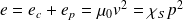
Vecteur densité surfacique de puissance sonore :
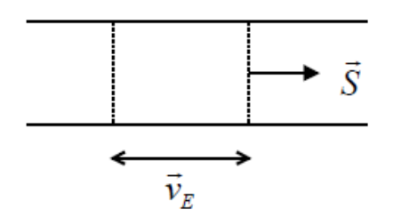
Vitesse de l'énergie :
On considère un tuyau sonore de section S et on va calculer de deux manières différentes l'énergie qui traverse la section
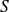pendant l'intervalle de temps
.L'énergie peut se calculer à partir du flux du vecteur
: 
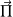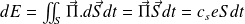
Elle peut se calculer en disant qu'elle était contenue dans le volume
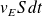, soit :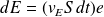 
En égalant ces deux expressions, on obtient que
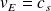. On retrouve le même résultat que pour les ondes EM dans le vide, pour lesquelles la vitesse de l'énergie est égale à la vitesse de propagation des ondes dans le vide, soit
.
Définition : Intensité acoustique
La sensation auditive sonore (ou intensité sonore) dépend du spectre de fréquence, de la durée et surtout de l'intensité du son.
En général, l'intensité d'une onde élastique est proportionnelle, à la fois, au carré de la fréquence et au carré de l'amplitude.
En termes de pression acoustique, l'intensité du son est proportionnelle au carré de l'amplitude
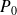de l'onde de pression.
L'intensité des sons naturels varie énormément et l'oreille humaine est sensible à une très large plage de variation de l'intensité.
On peut supporter des intensités jusqu'à environ
, qui correspond un son tellement fort qu'on commence à ne plus entendre ; c'est le seuil de douleur et il correspond à une pression acoustique d'environ seulement 10 Pa.
A l'autre extrême, l'oreille détecte juste des sons d'intensité aussi faible que
.
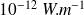C'est le seuil d'audibilité, qui est associé à une pression acoustique de l'ordre de
.
Rayleigh a montré qu'à 1 kHz, cette pression acoustique correspond à une vibration des molécules d'air de l'ordre de
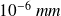seulement.
L'oreille humaine opère sur un large domaine qui correspond à un facteur d'un million (de
. à
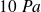) pour la pression et un facteur égal au carré de cette quantité pour l'intensité sonore, soit
.
C'est une plage de fonctionnement très étendue pour un détecteur.
Elle est équivalente à celle d'un dispositif capable de mesurer, à la fois, le diamètre d'un atome et la longueur d'un terrain de football.
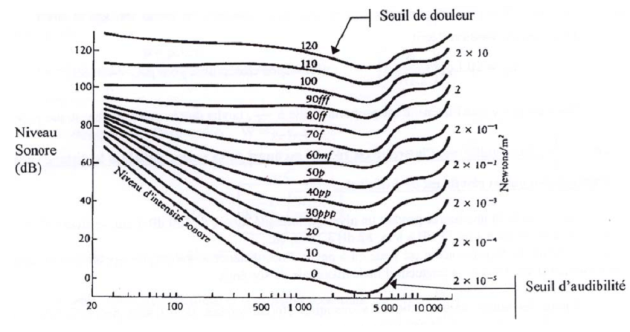
La figure montre les limites de la sensibilité de l'oreille en fonction de la fréquence.
Lorsque l'on écoute deux sons, on juge leur volume relatif, non par la différence des intensités mais par le rapport des intensités.
Une multiplication de l'intensité d'un son par 10 sera généralement perçue comme une multiplication du volume par 2.
Ainsi un son d'intensité
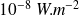est perçu comme deux fois plus fort qu'un son d'intensité
et
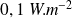est perçu comme deux fois plus fort que
.
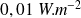Cela équivaut à dire que l'oreille est sensible au logarithme de l'intensité.
On définit l'intensité sonore (ou acoustique) en décibels (dB) :
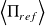correspond au seuil auditif pour une fréquence de référence de 1 000 Hz.
Le seuil de douleur correspond approximativement à une intensité sonore de 120 dB.
Quelques ordres de grandeur :
Pièce silencieuse : 30 dB
Lave-vaisselle silencieux : 50 dB
Rue animée : 75 dB
Cantine scolaire : 100 dB
Avion : 120 dB
Boîte de nuit : 130 dB
Fusée : 180 dB
