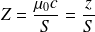Impédances acoustiques
Fondamental : Calcul de l'impédance acoustique
On considère une onde sonore plane progressive harmonique (OPPH) se propageant dans le sens croissant
.
La vitesse et la surpression peuvent s'écrire :
Et :
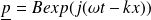
Avec la relation de dispersion :
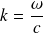
où
est la vitesse des ondes sonores.
L'équation suivante (voir fiche de cours sur les ondes sonores) :
permet de déterminer une relation entre la vitesse et la surpression.
En effet :
Soit :
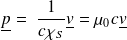
Attention : Définition de l'impédance acoustique
Pour une OPPH se déplaçant dans le sens des
: 
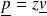
Avec :
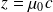
est appelée impédance acoustique.Pour une OPPH se déplaçant dans le sens des
: 
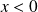Remarque : Autre définition de l'impédance acoustique
On peut définir l'impédance acoustique selon :
où
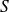désigne la section transverse de la conduite sonore.
Cette définition est similaire à celle de la résistance électrique : le débit
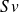est comparable à l'intensité électrique (débit de charges).
L'impédance acoustique définie ainsi vaut :
