Ondes acoustiques
Définition : Approximation acoustique
L'expérience montre que la propagation des ondes sonores est généralement caractérisée par un faible amortissement au sein du fluide où elles se propagent.
On négligera donc les phénomènes dissipatifs (conduction thermique et viscosité), ce qui revient à postuler le caractère isentropique de la propagation des ondes sonores et donc à supposer le fluide parfait.
Les seules forces prises en compte sont les forces de pression (la pesanteur est négligée).
Soient
,
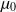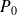et
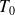les caractéristiques du fluide au repos (supposées uniformes), on note :
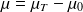, la variation de masse volumique du fluide (
)
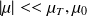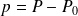, la variation de pression du fluide, encore appelée surpression acoustique (
)
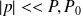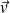le vecteur vitesse d'une particule de fluide (nul au repos)
L'approximation acoustique consiste à considérer que les grandeurs
,
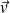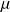e t
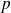sont des infiniment petits du même ordre (ainsi que leurs dérivées spatiales et temporelles).
Notamment, les calculs seront effectués à l'ordre 1 en ces infiniment petits.
Ordre de grandeur de la surpression :
Les surpressions susceptibles d'être détectées par une oreille varient typiquement de 100 Pa (son douloureux) à 10 – 5 Pa (seuil d'audition), couvrant ainsi 7 décades.
Fondamental : Hypothèse d'adiabaticité
La propagation du son dans un fluide peut être étudiée en considérant que le fluide effectue de petits mouvements isentropiques.
Dans le cadre de l'approximation acoustique, le coefficient de compressibilité isentropique donne :
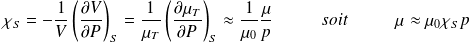
Méthode : Linéarisation des équations de conservation de la masse et de l'équation d'Euler
L'équation de conservation de la masse s'écrit :
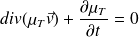
Soit, avec
: 
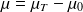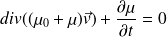
D'où :
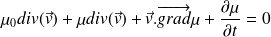
Approximation linéaire (ou acoustique) : on se limite dans la suite aux termes du 1er ordre.
Par conséquent :
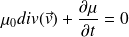
L'équation du mouvement du fluide est ici l'équation d'Euler (pas de viscosité) :
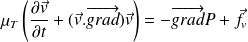
La force volumique statique (par exemple,
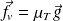) est compensée par le gradient de la pression statique
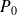. L'influence de ses variations (par exemple
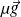) est en pratique négligeable par rapport au gradient de la surpression
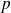. L'équation du mouvement devient alors, après linéarisation :
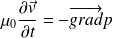
On rappelle de plus la relation entre la surpression et la variation de la masse volumique :
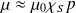
En éliminant la variable
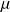, on obtient le système d'équations couplées :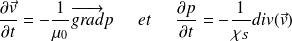 
Fondamental : Équation de propagation
Pour la surpression
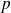: On calcule la divergence de l'équation de gauche précédente :
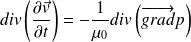
Soit :
On reconnaît l'équation de propagation de d'Alembert ; la vitesse des ondes sonores s'en déduit :
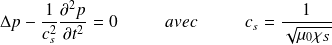
Pour la vitesse
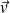: En écrivant que :
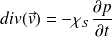
Puis en en prenant le gradient tout en dérivant l'équation :
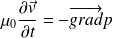
Par rapport au temps :
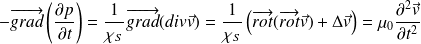
Très souvent, on aura un champ des vitesses de la forme
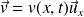, par conséquent
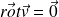. Ce résultat peut se généraliser.L'équation vérifiée par le champ des vitesses devient :
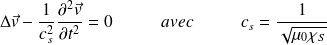
On retrouve une relation de d'Alembert identique à celle obtenue pour la surpression.
Attention : Équations de d'Alembert pour la surpression et le champ des vitesses
Exemple : Ordre de grandeur de la vitesse du son dans l'air
Pour un gaz parfait en évolution isentropique, la loi de Laplace permet d'écrire :
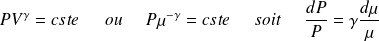
Soit, en utilisant l'hypothèse acoustique :
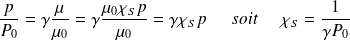
La vitesse du son devient :
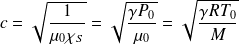
Où
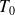est la température du gaz à l'équilibre et M sa masse molaire.
AN :
Avec
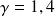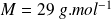et
et
:
.
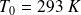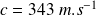Remarque :
Pour un liquide,
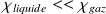: la vitesse du son est donc plus importante dans les liquides que dans les gaz.Le cas des solides n'entre pas dans le cadre de l'étude menée ici (Voir le modèle de la chaîne d'atomes couplés par des ressorts).
On remarque toutefois que la vitesse du son dans un solide est encore plus élevée que dans un liquide.
Complément : Une vidéo sur le résonateur de Helmholtz
Pourquoi souffler dans une bouteille fait naître un son ?
Animations Java (par JJ.Rousseau, Université du Mans) : le résonateur de Helmholtz - Cliquer ICI
