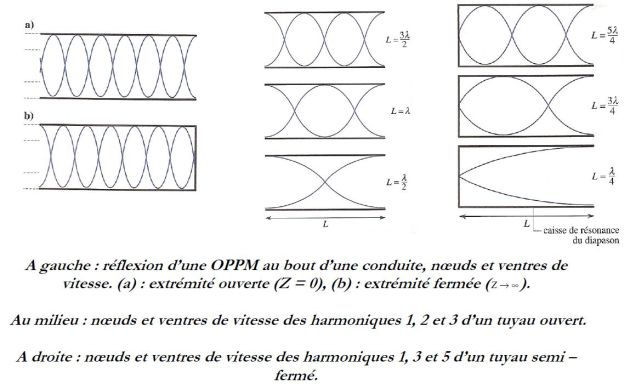
Réflexion et transmission des ondes sonores
Méthode : Relations de passage à la traversée d'un dioptre sonore
On s'intéresse à la réflexion et à la transmission d'une onde progressive sous incidence normale.
Les milieux (1) et (2) ont des caractéristiques physiques a priori différentes mais la pression à l'équilibre est identique, notée
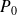 .
.
Une surface qui délimite deux milieux différents est appelée "dioptre acoustique".
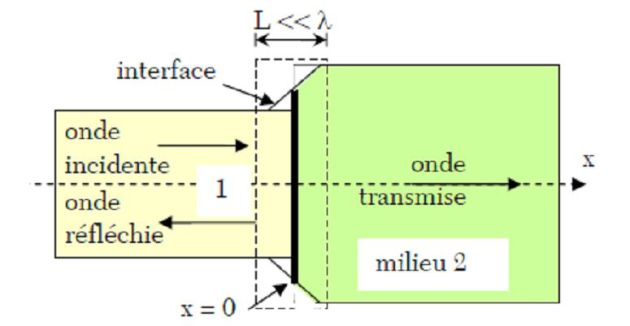
On étudie la réflexion et la transmission d'ondes sonores planes au niveau du raccordement de deux conduites de sections S1 et S2, séparant deux milieux matériels d'impédances caractéristiques
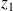 pour
pour
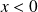 et
et
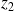 pour
pour
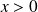 .
.
On rappelle que l'impédance acoustique est définie à partir de :
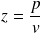
On note :
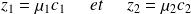
Continuité du débit volumique à l'interface :
On considère que les deux fluides ne se mélangent pas, de telle sorte que l'interface constitue une membrane imperméable.
Soit V un volume dans la zone de raccordement, compris entre les deux sections droites
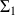 et
et
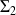 , situées en
, situées en
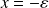 et
et
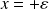 .
.
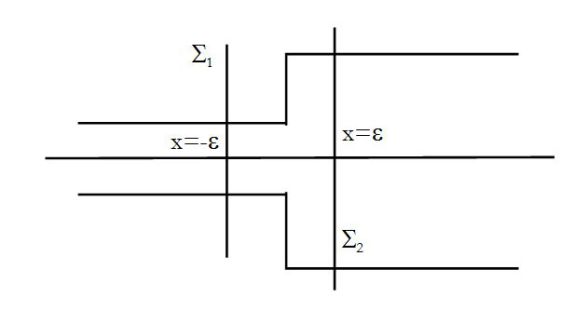
On peut imaginer le volume (V) qui oscille de part et d'autre de la membrane de séparation et écrire directement la conservation du volume, ce qui donne la conservation du débit volumique :
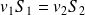
Dans le cas particulier où les deux sections sont égales, il y a alors continuité de la vitesse de part et d'autre de la membrane.
Continuité de la surpression :
Dans l'approximation acoustique, le déplacement de l'interface est faible devant la longueur d'onde et peut être négligé, de sorte que l'interface reste confondue avec le plan
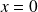 .
.
On suppose que la pression au repos a la même valeur
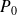 en tout point de l'espace.
en tout point de l'espace.
En considérant un élément de surface dS de l'interface entre les deux fluides comme une membrane fictive de masse nulle, on montre à l'aide du principe fondamental de la dynamique en projection sur Ox que la surpression est continue à l'interface.
En effet :
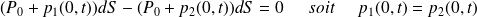
Remarque :
Dans le cas où l'interface est assimilée à une plaque plane de masse surfacique
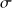 , la relation entre les surpressions de part et d'autre de l'interface s'écrit maintenant :
, la relation entre les surpressions de part et d'autre de l'interface s'écrit maintenant :
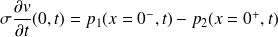
Fondamental : Coefficients de réflexion et de transmission en amplitude
On suppose que les deux sections sont identiques :
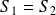
On considère que l'onde incidente est une OPPH :
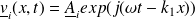
Les ondes réfléchie et transmise sont notées :
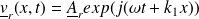
Et :
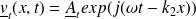
Les vecteurs d'onde sont donnés par :
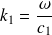
Et :
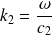
où
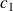 et
et
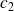 sont les vitesses du son dans les deux milieux.
sont les vitesses du son dans les deux milieux.
Les surpressions s'en déduisent en utilisant la relation
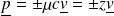 , soit :
, soit :
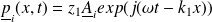
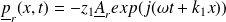
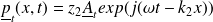
Utilisation des relations de passage :
Continuité du débit volumique à l'interface en
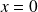 (continuité de la vitesse puisque les sections sont identiques) :
(continuité de la vitesse puisque les sections sont identiques) : 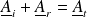
Continuité de la surpression à l'interface en
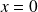 :
: 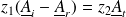
Expression des coefficients de réflexion et de transmission en amplitude :
Le système précédent se résout sous la forme :
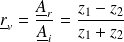
Et :
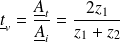
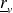 est le coefficient de réflexion en amplitude pour la vitesse et
est le coefficient de réflexion en amplitude pour la vitesse et
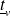 est celui en transmission pour la vitesse également.
est celui en transmission pour la vitesse également.
Les coefficients de réflexion et de transmission pour la pression s'en déduisent :
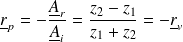
Et :
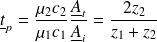
Quelques remarques :
Les coefficients de transmission (
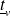 et
et
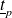 ) sont réels positifs : l'onde transmise est toujours en phase avec l'onde incidente.
) sont réels positifs : l'onde transmise est toujours en phase avec l'onde incidente.Les coefficients de réflexion peuvent être positifs ou négatifs : l'onde réfléchie peut être en phase ou en opposition de phase avec l'onde incidente.
Lorsque
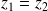 , il n'y a pas d'onde réfléchie (on parle d'adaptation d'impédances).
, il n'y a pas d'onde réfléchie (on parle d'adaptation d'impédances).L'onde sonore dans le milieu (1) résulte de la superposition de deux OPPH se propageant en sens inverse et dont les aplitudes sont en général différentes.
Il ne s'agit pas ni d'une onde progressive ni d'une onde stationnaire, mais d'une onde ayant un certain TOS (taux d'onde stationnaire).
Dans le cas particulier où
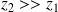 :
: 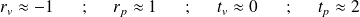
Il n'y a plus d'onde transmise. On montre que l'on obtient des ondes stationnaires dans le milieu (1) avec nœud de vitesse et ventre de pression en
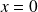 .
.C'est le cas d'une interface air vers solide.
Si
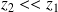 , alors :
, alors : 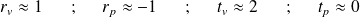
Il n'y a plus d'onde transmise. On obtient toujours des ondes stationnaires dans le milieu (1) mais avec un ventre de vitesse et un nœud de pression en
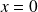 .
.C'est le cas d'une interface solide vers air.
Fondamental : Coefficients de réflexion et de transmission en énergie
En valeur moyenne, les vecteurs "densité surfacique de puissance sonore" des trois ondes incidente, réfléchie et transmise sont :
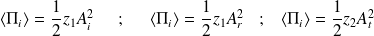
On en déduit les coefficients de réflexion et de transmission en énergie :
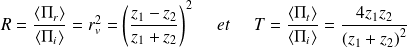
Remarques :
Conservation de l'énergie :
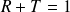
Quand
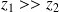 ou
ou
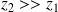 ,
,
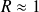 et
et
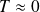 : il n'y a pas d'onde transmise.
: il n'y a pas d'onde transmise.Pour
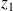 donnée, le coefficient
donnée, le coefficient
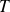 est maximal quand
est maximal quand
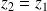 : il y a adaptation d'impédances.
: il y a adaptation d'impédances.Une interface ne transmet correctement les ondes sonores que si les impédances de part et d'autre sont voisines.
Par exemple, un plongeur entendra distinctement le bruit d'une hélice de hors-bord tournant dans l'eau mais beaucoup plus difficilement une personne placée sur la berge lui ordonnant de faire attention.
Complément : Instruments de musique (trompettes, tuyaux d'orgue, ...)
Ondes stationnaires et harmoniques
Complément : Un peu de musique : ondes sonores stationnaires
Dans le cas d'un dioptre acoustique entre deux milieux identiques mais avec des sections
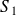 et
et
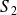 différentes, on aboutit aux coefficients de réflexion et de transmission en amplitude pour la vitesse et la surpression suivants :
différentes, on aboutit aux coefficients de réflexion et de transmission en amplitude pour la vitesse et la surpression suivants :
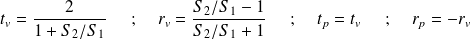
On en déduit que :
Pour un tuyau (d'orgue par exemple) ouvert à une extrémité (alors
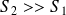 ) :
) : Il y a un nœud de surpression et un ventre de vitesse à l'extrémité.
Pour un tuyau fermé à une extrémité (
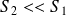 ) :
) : Il y a un nœud de vitesse et un ventre de surpression à l'extrémité.
Fréquences dans un tuyau sonore :
Les extrémités du tuyau sont de même nature :
La longueur du tuyau doit être un multiple entier de la distance entre deux nœuds (ou deux ventres), soit un multiple entier de la demi-longueur d'onde.
La fréquence du mode fondamental est alors
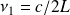 , où
, où
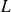 est la longueur du tuyau et
est la longueur du tuyau et
 la vitesse du son.
la vitesse du son.Les fréquences des différents harmoniques sont les multiples pairs et impairs du fondamental.
Les extrémités du tuyau sont de nature différente :
La longueur du tuyau doit être un multiple entier de la demi-longueur d'onde
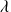 augmentée de
augmentée de
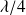 .
.La fréquence du mode fondamental est alors
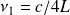 , où
, où
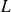 est la longueur du tuyau et
est la longueur du tuyau et
 la vitesse du son.
la vitesse du son.Les fréquences des différents harmoniques sont les multiples impairs seulement du fondamental.