Incertitudes de type B
Fondamental : Estimation statistique (type B)
Si l'on ne dispose pas d'une série de mesures, il faut estimer l'incertitude sur la grandeur à partir du processus expérimental.
Lorsque l'on mesure une grandeur avec un appareil, cela revient à estimer la probabilité que la valeur affichée corresponde à la valeur vraie.
On fait intervenir des lois de probabilités supposées a priori en s'appuyant sur une certaine connaissance des grandeurs d'influence, sur les spécifications fournies par le constructeur d'un appareil de mesure, sur l'incertitude assignée à des valeurs de références fournies par des livres, ...
Dans le cas le plus fréquent, on suppose que la vraie valeur de
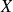se trouve à coup sûr dans un certain intervalle
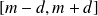avec une densité de probabilité uniforme de la forme :
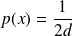
C'est le cas par exemple :
Quand un constructeur fournit une indication du type
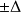ou
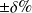.Quand on connaît la "classe" de l'instrument (un voltmètre, par exemple) : l'erreur maximale est fournie par un pourcentage de l'indication maximale que peut donner l'instrument.
Un dernier exemple est donné par la résolution finie des indicateurs numériques qui ne peuvent afficher que des valeurs quantifiées.
L'incertitude-type se calcule alors selon la relation :
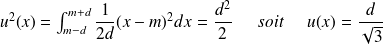
Exemples :
Une résistance est annoncée par le constructeur à
. On choisit dans ce cas comme incertitude-type :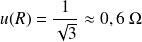 
Une fiole jaugée porte l'inscription
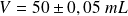. On choisit comme incertitude-type associée :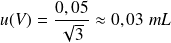 
On fait une mise au point sur un banc d'optique. Toutes les positions
dans l'intervalle
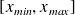semblent donner une image nette. On peut poser :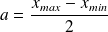 
On choisit alors comme résultat de mesure :
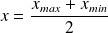
et comme incertitude-type associée :
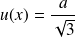
On mesure une tension
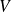à l'aide d'un voltmètre numérique. Le voltmètre est réglé sur le calibre 400 mV. L'écran affiche 203,1 mV.Le manuel du voltmètre indique que dans ce calibre, l'appareil est précis à
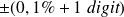.La tolérance vaut donc ici :
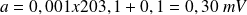
On prendra alors comme incertitude type :
