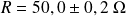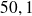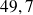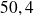Incertitudes de type A
Définition : Un glossaire de métrologie
Erreur de mesure :
Résultat d'un mesurage moins la valeur vraie du mesurande.
Erreur aléatoire :
Lorsque l'on répète N fois le même mesurage dans des conditions aussi identiques que possible, on obtient une série de mesures
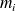a priori différentes. Les fluctuations des mesures
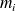autour de leur valeur moyenne
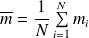constituent l'erreur aléatoire. Cette erreur a pour origine les fluctuations du dispositif expérimental que l'on ne contrôle pas (fluctuations de température, d'humidité, imprécisions de manipulation, ...).
Plus l'erreur aléatoire est faible et plus le mesurage est fidèle.
Erreur systématique :
Un défaut dans le processus expérimental peut conduire à une déviation de la valeur attendue du mesurande allant toujours dans le même sens.
Par exemple, mesurer des distances avec un mètre ruban qui a été trop étiré conduira à des mesures de distances sous-estimées.
Plus l'erreur aléatoire est faible et plus le mesurage est dit juste.
La figure suivante illustre les notions de mesurage fidèle ou juste.
Pour la 1ère cible : mesurage ni fidèle ni juste.
Pour la 2ème cible : mesurage fidèle mais peu juste.
Pour la 3ème cible : mesurage peu fidèle mais juste.
Pour la 4ème cible : mesurage fidèle et juste.
Grandeur d'influence :
Grandeur qui n'est pas le mesurande mais qui a un effet sur le résultat du mesurage.
Mesurande :
Grandeur particulière soumise à mesurage.
Mesurage :
Ensemble d'opérations ayant pour but de déterminer une valeur d'une grandeur.
Valeur vraie d'une grandeur :
Valeur compatible avec la définition de cette grandeur. C'est celle que l'on obtiendrait par un mesurage parfait.
Elle est par nature inconnue.
Incertitude :
Paramètre associé au résultat d'un mesurage, qui caractérise la dispersion des valeurs qui pourraient raisonnablement être attribuées au mesurande.
Définition : Incertitudes de type A ou B
On ne tient compte que des erreurs aléatoires.
Deux cas peuvent alors se présenter :
On réalise un grand nombre de mesures : on effectue alors une évaluation statistique de l'incertitude.
On parle alors d'estimation de l'incertitude de type A.
Si l'évaluation statistique n'est pas possible, on parle alors d'incertitude de type B.
C'est par exemple le cas quand on mesure une position sur un banc d'optique gradué.
Fondamental : Estimation statistique (type A)
On a effectué une série de
mesures
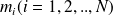dans les mêmes conditions et indépendantes les unes des autres.
Le résultat de mesure, noté m, sera la moyenne de ces mesures :
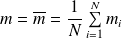
On définit l'écart-type expérimental (calculable avec une calculatrice) :
Cette quantité caractérise la variabilité des valeurs observées pour le mesurande choisi.
Le résultat de mesure n'est pas estimé à partir d'une valeur unique
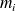choisie dans la série mais par la moyenne
.
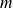Pour exprimer l'incertitude sur le résultat, ce n'est donc pas l'incertitude-type de
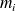qu'il faut choisir, mais celle de la moyenne
.
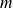Celle-ci sera moins élevée. On la note
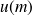et elle est donnée par :
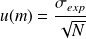
On remarque que plus le nombre de mesures est élevé et plus l'incertitude-type sur
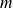est faible.
Cette relation n'est cependant pas linéaire : multiplier par 100 le nombre de mesures ne divise l'incertitude-type que par 10.
Exemple : Mesures d'une résistance
On a mesuré 10 fois la même résistance avec le même ohmmètre.
Les mesures sont supposées être indépendantes.
On obtient :
|
|
|
|
|
|
|
|
|
|
|
La valeur moyenne vaut :
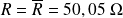
L'écart-type expérimental vaut :
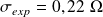
L'incertitude type sur la résistance est donc :
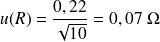
L'incertitude élargie (voir fiche de cours sur l'incertitude élargie, avec un niveau de confiance de 95%) est choisie selon :
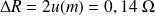
On se limite à un chiffre significatif pour l'incertitude, soit, en surestimant le résultat :
On fait ensuite correspondre le dernier chiffre significatif de la mesure à l'incertitude.
Finalement :
