Propagation des incertitudes
Fondamental : Cas de la somme m=x+y
On souhaite évaluer l'incertitude élargie sur la somme :
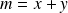
connaissant les incertitudes élargies sur
et
.
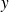On montre que :
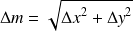
Les incertitudes s'ajoutent en quadrature.
Remarques :
L'addition en quadrature présente l'avantage de ne pas surestimer l'incertitude.
Ce résultat est vrai si les variables
et
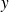sont indépendantes.
Fondamental : Cas général : m=f(x,y)
On souhaite évaluer l'incertitude élargie sur la pulsation de résonance d'un circuit série RLC :
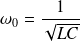
connaissant les incertitudes élargies
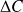et
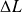sur les valeurs de la capacité et de l'inductance.
D'une manière générale, on souhaite évaluer l'incertitude sur la grandeur
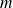reliée à
et
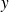par une loi générale :
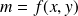
Si les variables
et
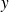sont indépendantes, on montre que :
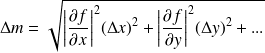
Exemple de la pulsation de résonance :
On calcule les dérivées partielles :
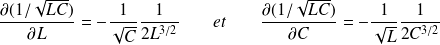
Par conséquent :
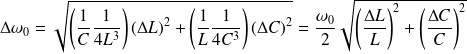
Ou encore :
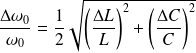
Les incertitudes
,
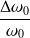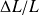et
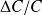sont appelées incertitudes relatives.
Utilisation de la dérivée logarithmique :
On peut écrire :
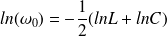
Et différentier :
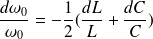
On en déduit alors directement :
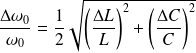
Fondamental : Généralisation de la dérivée logarithmique
La formule précédente peut se généraliser à tout produit ou quotient de la forme :
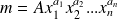
où A est une constante.
L'incertitude relative
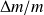vaut :
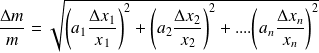
Exemple :
Lors de l'expérience des fentes d'Young, on a mesuré la distance
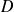entre les fentes et l'écran :
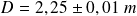
La longueur d'onde choisie est :
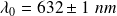
L'interfrange mesuré à l'aide d'un viseur de Fresnel muni de son vernier est :
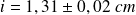
On souhaite en déduire la distance
entre les fentes et son incertitude élargie associée.
La valeur choisie pour
est donnée par :
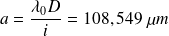
L'incertitude relative est donnée par :
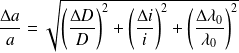
On trouve :
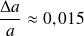
Et ainsi :
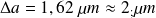
Finalement :
