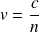Principe de Fermat
(10 minutes de préparation)
Pierre de Fermat (mathématicien et physicien français, 1601-1665) postula que les rayons lumineux répondaient à un principe très général selon lequel le chemin emprunté par la lumière pour se rendre d'un point donné à un autre était celui pour lequel le temps de parcours était minimum (en fait un extremum qui peut être un minimum ou un maximum).
Un maître nageur, situé en un point A d'une plage, souhaite appliquer ce principe afin de porter secours le plus rapidement possible à un vacancier (situé en B) sur le point de se noyer à quelques brasses du bord de mer.
On note
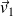et
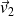les vecteurs vitesses (supposés constants) du maître nageur sur la plage (lorsqu'il court) et dans l'eau (où il nage).
Question
Quel doit être le chemin suivi par le maître nageur afin que le principe de Fermat soit vérifié et le vacancier sain et sauf ?
En déduire l'expression de la loi de la réfraction en optique.
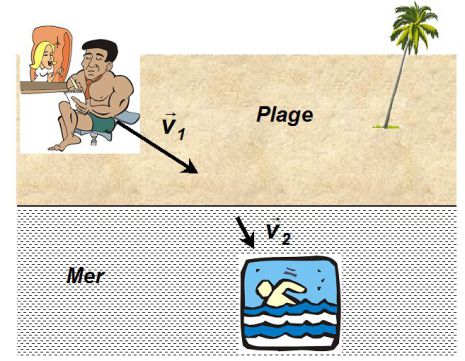
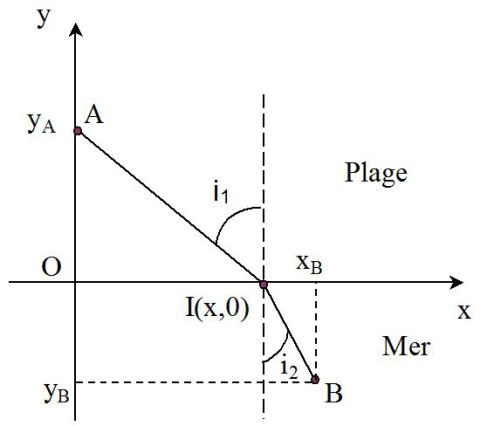
On choisit un repère qui simplifie le problème : on fait passer l'axe des abscisses par la droite qui sépare la plage de la mer et l'axe des ordonnées par le point A, position initiale du maître nageur.
Dans un tel repère, les points A et B ont alors les coordonnées A (0,yA) et B (xB,yB).
La trajectoire du maître nageur va être constituée de deux portions rectilignes AI et IB, où I (x,0) désigne le point où le maître nageur se met à nager.
On peut remarquer que la distance AI sera plus grande que la distance IB puisque le maître nageur va certainement plus vite en courant qu'en nageant !
Le temps T mis pas le maître nageur pour aller de A à B est alors :
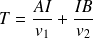
En développant les valeurs de AI et IB, on obtient la dépendance suivante de T = T(x) en fonction de l'abscisse x de I :
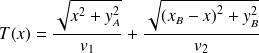
L'extremum de T(x) est atteint lorsque sa dérivée par rapport à x est nulle. Or :
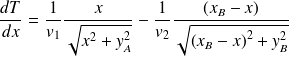
En remarquant que :
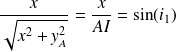
Et :
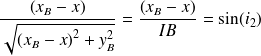
(où les angles i1 et i2, par analogie avec l'optique (voir figure ci-dessus), peuvent être appelés angle d'incidence et angle de réfraction), la condition d'un temps extremum mis par la lumière (soit ) s'exprime alors sous la forme :
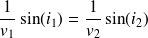
Il suffit que les angles d'incidence et de réfraction remplissent cette condition pour que le chemin parcouru par le maître nageur soit effectivement celui qui prend le moins de temps.
Il est en effet évident que ce temps extrémal correspond bien à un minimum ; en effet, la distance AI et donc le temps T peuvent être facilement rendus très grands si le maître nageur, manquant alors assurément de conscience professionnelle, décidait d'aller par exemple faire des courses avant de porter secours au pauvre vacancier !
Complément : Cas de la lumière et lois de Snell-Descartes :
On considère deux milieux (M1) et (M2) d'indices de réfraction respectifs n1 et n2.
Soient deux points A et B situés respectivement dans le milieu d'indice n1 (le point A) et dans le milieu d'indice n2 (le point B).
Le principe de Fermat permet d'affirmer que le chemin emprunté par la lumière pour aller de A à B est tel que le temps mis pour le parcourir est extremum (le plus souvent minimum).
Par application de ce principe, un raisonnement similaire à celui effectué dans le cas du chemin suivi par le maître nageur, permet de démontrer la loi de la réfraction énoncée, vers 1620, par les physiciens Snell et Descartes :
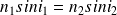
Où i1 et i2 sont respectivement les angles d'incidence et de réfraction (on rappelle que l'indice d'un milieu permet de connaître la vitesse v de la lumière dans ce milieu en fonction de celle dans le vide c :
