Théorème de Malus, superposition d'une onde plane et d'une onde sphérique
(20 minutes de préparation)
On utilise une lentille convergente (L), trouée en son centre, comme système interférentiel à deux ondes.
Une source ponctuelle S, monochromatique de longueur d'onde λ0, est placée au foyer objet F de la lentille.
Il en résulte que l'onde émergeant de la lentille est plane et que celle directement transmise par le trou est sphérique.
Le trou a un diamètre 2R = 10 mm sur la face de sortie de (L) et une profondeur e = 3 mm sur l'axe.
Question
Donner les expressions analytiques des ondes qui se superposent ; on adoptera comme origine la phase des ondes en S et on supposera que ces deux ondes ont même amplitude.
La source est au foyer de la lentille : elle émet une onde sphérique. La lentille la transforme en onde plane.
Le chemin optique δ1 pour aller de S à M en passant par la lentille est égal à celui pour aller de S à F' (utiliser le théorème de Malus) en passant par O. Par conséquent :
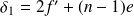
L'expression de l'onde plane en M est donc :
Pour l'onde sphérique qui va directement de F à M, le chemin optique est (avec r << f') :
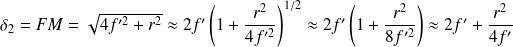
L'amplitude de l'onde sphérique est :
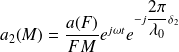
Soit, en supposant que cette onde a même amplitude que l'onde plane :
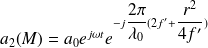
L'amplitude résultante en M est donc :
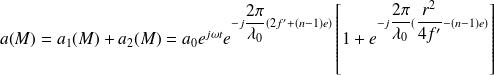
Question
Quelle est l'intensité, dans le plan P situé à la même distance f' de la face de sortie de (L) que S, en fonction de la coordonnée cylindrique r ?
En déduire la nature des franges d'interférences.
L'intensité résultante est :
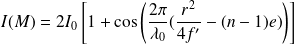
Les franges sont ici des anneaux (correspondant à r = cste) centrés sur F'. Un rayon brillant est donné par :
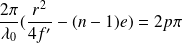(Avec p entier)
Soit :
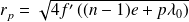
Question
Calculer le rayon des franges brillantes extrêmes sachant que la longueur d'onde du rayonnement est λ0 = 546 nm, f' = 20 cm et n = 1,52 (indice du verre de (L)).
Le point M est dans le champ d'interférences si
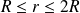. On calcule p en prenant r = R puis en prenant r = 2R.
On trouve p = - 2 800 et p = - 2 628,2.
Dans ce dernier cas, il faut prendre p = - 2 629 et recalculer r. On trouve r = 9,98 mm.
