Mécanique et poussée d'Archimède, modèle d'atmosphère et stabilité
Consacrer 20 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
On considère que l'atmosphère est un gaz parfait soumis au champ de pesanteur uniforme et présentant une température variant avec l'altitude suivant une loi :
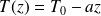(avec
)
Question
Paramètres décrivant l'atmosphère
Déterminer l'évolution de la pression en fonction de l'altitude.
Montrer qu'il existe une relation du type
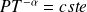entre la pression et la température en un point donné, α étant un paramètre lié à a et aux caractéristiques du gaz.
Le résultat est classique (voir cours) :
On voit que :
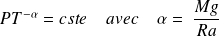
Question
Stabilité de l'atmosphère
Soit une "bulle" d'air en équilibre à l'altitude z0.
Elle se déplace de δz sous l'action d'une perturbation (δz << z0).
On suppose que la transformation de la bulle est adiabatique quasi statique et que la bulle est en équilibre de pression avec l'air extérieur situé à son niveau.
A quelle condition peut-on considérer que la bulle est en équilibre stable à l'altitude z0 ?
On notera
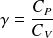, rapport qui sera considéré comme constant.
Comparer le poids de la bulle avec la poussée d'Archimède.
A la cote
, la bulle est soumise à son poids et à la poussée d'Archimède, de résultante :
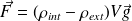
Or (loi des gaz parfaits) :
Ainsi :
Si le déplacement
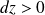, cette force correspondra à une force de rappel (et donc équilibre stable) si
.
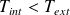Or, à l'intérieur de la bulle, la transformation est adiabatique réversible et donc :
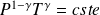
Soit :
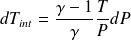
A l'extérieur, on aura
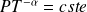, soit :
L'équilibre est stable si
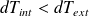, soit :
