Effet de peau dans un conducteur ohmique plongé dans un solénoïde
Consacrer 20 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Un solénoïde cylindrique d'axe (Oz) de rayon R0 comportant n spires par mètre est parcouru par un courant variable dont l'intensité est i(t) = I cos (ωt).
On admet que le champ magnétique propre créé par le solénoïde est uniforme à l'intérieur (r < R0) :
Et nul à l'extérieur (r > R0) et que le champ électrique est orthoradial :
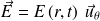
Question
Déterminer le champ électrique à l'intérieur du solénoïde.
Quelle est la relation de Maxwell qui permet d'expliquer pourquoi apparaît un champ électrique quand un champ magnétique dépend du temps ?
Penser au théorème de Stockes.
On utilise l'expression intégrale de l'équation de MF (obtenue avec le théorème de Stokes) :
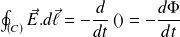
Avec les hypothèses de l'énoncé :
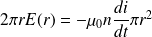
Soit :
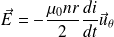
Question
On place un cylindre massif long de conductivité
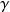, de hauteur h et de rayon R1 < R0 à l'intérieur du solénoïde.
Déterminer la densité de courant
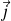créée par le champ électrique
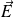. Quel est l'effet observable associé à ces courants ?
Loi d'Ohm locale donne :
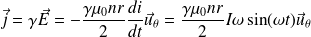
Échauffement dû à l'effet Joule :
On calcule la puissance volumique :
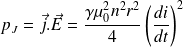
Question
En déduire le champ magnétique
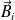créé sur l'axe par les courants et donner la condition sous laquelle ce champ (appelé champ induit) est négligeable devant celui créé par le solénoïde
On a des solénoïdes emboîtés ; pour un solénoïde situé entre r et r + dr, le champ magnétique sur l'axe est :
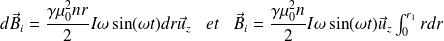
Finalement :
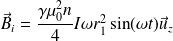
On évalue le rapport des deux champs magnétiques :
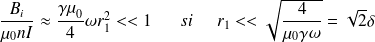
Soit r1 << l'épaisseur de peau
.
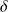Question
Si cette condition n'est pas vérifiée, indiquer sans justification la répartition des courants dans le cylindre.
On a effet de peau et le courant n'existe que sur la partie périphérique du cylindre de l'ordre de quelques
.
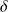