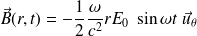Condensateur alimenté à haute fréquence
Consacrer 30 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Un condensateur plan, constitué de deux plaques circulaires d'axe (Oz) et de rayon R, séparées par une distance e faible devant R, est alimenté par un générateur de tension sinusoïdale de pulsation ω.
Question
Pour ce système à symétrie cylindrique, on écrira le champ électrique sous la forme :
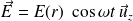
Quelle est l'équation différentielle vérifiée par la fonction E(r) ?
Déterminer la solution sous la forme d'une série entière développée en puissances de la variable sans dimension
.
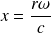Donnée :
En coordonnées cylindriques, le laplacien d'une fonction est :
Redémontrer l'équation de propagation du champ électrique dans le vide (équation de d'Alembert) puis utiliser là ...
Le champ électrique vérifie, en l'absence de courants et de charges :
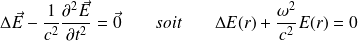
Avec l'expression précédente du laplacien, il vient :
Soit :
On pose :
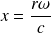
Et on cherche une solution de la forme (E0, valeur du champ sur l'axe (Oz)) :
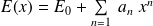
Alors :
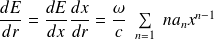
Et :
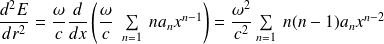
Par conséquent :
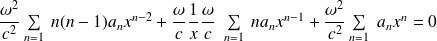
D'où :
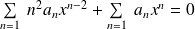
Soit :
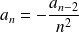
Avec :
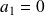(diverge en 0 sinon)
La solution recherchée est donc de la forme :
Question
On donne :
ω = 20π MHz et R = 5 cm.
Que peut-on dire de la fonction E(r) à l'intérieur du condensateur ?
L'ARQS est –elle convenable ?
On pose :
Le champ électrique peut s'écrire :
Le champ est pratiquement uniforme à l'intérieur du condensateur et vaut :
L'ARQS est bien vérifiée ; en effet, les retards sont bien négligeables vis-à-vis du temps caractéristique T :
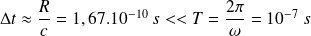
Par contre, si
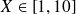, les termes de la série donnant E(r) ne sont pas négligeables et le champ E(r) n'est plus uniforme.
Question
Que vaut le champ magnétique à l'intérieur du condensateur ?
Dans le condensateur, le champ magnétique est, pour ce problème à géométrie cylindrique, de la forme :
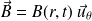
Le théorème d'Ampère généralisé indique que la circulation du champ magnétique sur un cercle de rayon r (r < R) et d'axe (Oz) est égale au flux du courant de déplacement à travers le disque correspondant, multiplié par
:
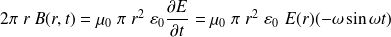
Soit :
Si l'ARQS est vérifiée, alors :
Et :
