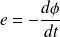Physical content of Maxwell's equations
Fondamental :
Maxwell's « local » equations give, after integrating, famous laws and theorems of electromagnetism.
They can be verified experimentally.
Let us begin with Gauss' law for electricity. The exiting flux of the electric field through a closed surface
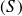 is expressed by :
is expressed by :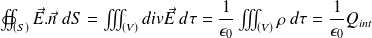
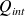 represents the charges inside the closed surface
represents the charges inside the closed surface
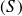 .
.Gauss' law appears to still be true in a non steady-state, even though the electric charges can be in motion.
In a steady-state, the sources of the electric field are the charges. They are characterized by their density
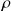 .
. The field lines diverge from positive charges, the same way a fluid exits a true source.
The field lines disappear on negative charges as a fluid in a pit.
This is still true in a non steady-state, except that
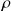 is not the only source of the electric field anymore (see the consequence of the Faraday's law of induction).
is not the only source of the electric field anymore (see the consequence of the Faraday's law of induction). Thus the electric field maps no longer look the same.
Let us calculate the linear integral of the magnetic field at a given moment around a closed loop
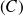 .
. On this loop is a surface
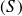 .
. Let's use Ampere's law :
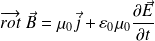
Thus :
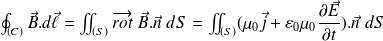
We recognize :
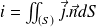
The intensity going through
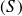 .
.In a non steady-state, this magnitude does not depend only on
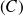 but also on surface
but also on surface
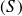 , because the flux of
, because the flux of
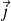 is no longer conserved.
is no longer conserved.So: (General Ampère's circuital law)
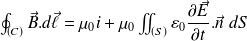
Hence the term :
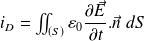
Can be interpreted as the flux of the displacement current through the surface
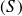 .
.Thus, in non steady-state, the sources of the magnetic field are of two kinds : the “real” currents and the displacement current, which comes from the time-dependence of the electric field.
In steady-state, we obviously retrieve Ampere's circuital law :
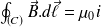
Equation of the magnetic flux (Conservation of the magnetic flux) :
The local equation
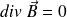 proves that (by using Green - Ostrogradsky's law) :
proves that (by using Green - Ostrogradsky's law) :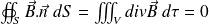
Hence :
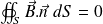
The flux of the magnetic field is conserved. Thus :
The magnetic flux is conserved at any time through any section of a field tube.
It is possible to define the magnetic flux that crosses a loop
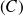 without any precision on the surface
without any precision on the surface
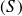 based on
based on
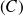 .
.
In comparison to Gauss' law of electricity, the magnetic field does not have any sources like the charges are to the electric field.
In other words, magnetic charges – or magnetic monopoles – do not exist.
Faraday's law of induction :
Let's evaluate the linear integral of the electric field around a closed loop
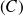 which supports a surface
which supports a surface
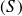 .
. Let us apply the Maxwell-Faraday equation :
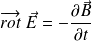
Under this form :
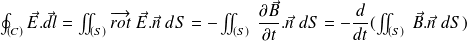
Let's write :
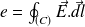
The electromotive force induced on the closed loop
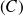 and :
and :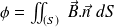
The flux of the magnetic field through a surface supported by
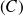 .
. It gives:
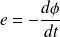
It is Faraday's law. It was experimentally found in 1831. It regulates electromagnetic induction phenomenons,
The circulation or the electric field is no longer equal to zero. The magnetic field changes in time and is the source of an electric field with a non conservative line integral.
Attention : Physical content of Maxwell's equations
Gauss' law of electricity :
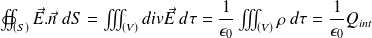
Ampere's circuital law :
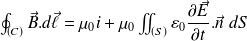
Conservation of the flux of the magnetic field :
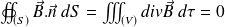
Faraday's law of induction :