Vector calculus
Fondamental : Field in physics
In physics, the term field denotes a physical quantity that is continuous function of position, within a certain region of space.
We distinguish scalar fields (such as temperature or electrostatic potential) from vector fields (such as the velocity of a moving fluid or the electric field
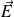 ).
).
A vector field assigns a direction, as well as a magnitude, to each point in space.
Since a vector can be represented by three components, a vector field is specified analytically by a set of three functions of position.
Since scalar and vector fields are functions of positions, they must have spatial derivatives and integrals.
Fondamental : Gradient operator
We consider first a scalar field
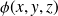 .
.
The rate of change in
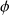 for small step away from the point
for small step away from the point
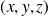 depends upon the direction of the step : the derivative operation has vectorlike properties.
depends upon the direction of the step : the derivative operation has vectorlike properties.
Specifically, for an infinitesimal step of magnitude
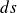 in the direction specified by the unit vector
in the direction specified by the unit vector
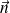 :
:
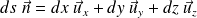
The change in
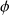 is :
is :
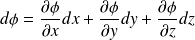
And :
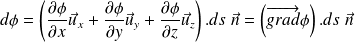
Where we introduce the gradient (or Nabla
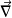 ) operator :
) operator :
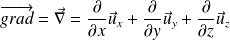
Thus the derivated of
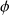 in the direction
in the direction
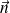 is :
is :
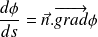
The vector field
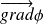 is the gradient of
is the gradient of
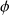 :
:
The gradient is thus a vector derivative, having the magnitude and direction of the greatest space rate of change of the scalar field
 .
.
The derivative in an arbitrary direction is simply the component of the gradient vector in that direction.
The gradient is directed perpendicular to the surface
 .
.
If the field is expressed in cylindrical or spherical coordinate systems, the forms of derivatives are altered but the meaning of the gradient is unchanged.
Cylindrical coordinate system :
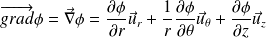
Spherical coordinate system :
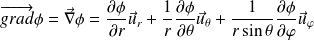
Fondamental : Divergence of a vector field
The divergence of a vector field :
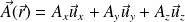
is defined by (in a cartesian coordinate system) :
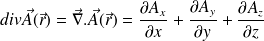
It can be proved that the divergence is the flux generation per unit volume.
Cylindrical coordinate system :
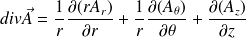
Spherical coordinate system :
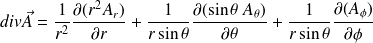
Green-Ostrogradsky theorem :
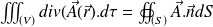
Where the finite closed surface
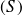 surrounds the finite volume
surrounds the finite volume
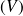 .
.
Fondamental : Curl (or rotation) of a vector field
The curl of a vector field is defined by (in a cartesian coordinate system) :
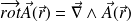
It means :
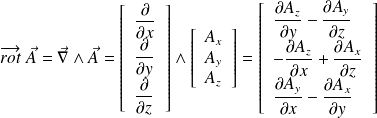
Cylindrical coordinate system :
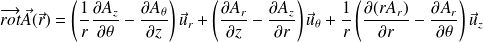
Spherical coordinate system :
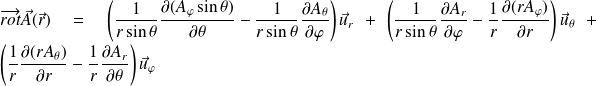
Stokes' theorem :
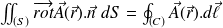
Where the closed loop
 bounds the finite open surface
bounds the finite open surface
 .
.
Fondamental : Laplacian of a scalar field
The laplacian of a scalar field
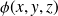 is defined by :
is defined by :
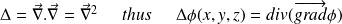
In a cartesian coordinate system :
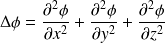
Fondamental : Physical interest of vector operators
We can illustrate the terms of divergence and curl for some types fields : (see figure below)
The divergence and the curl are zero for the field whose field lines are parallel.
The divergence is negative for fields whose field lines converge to a point. It is positive for a diverging field.
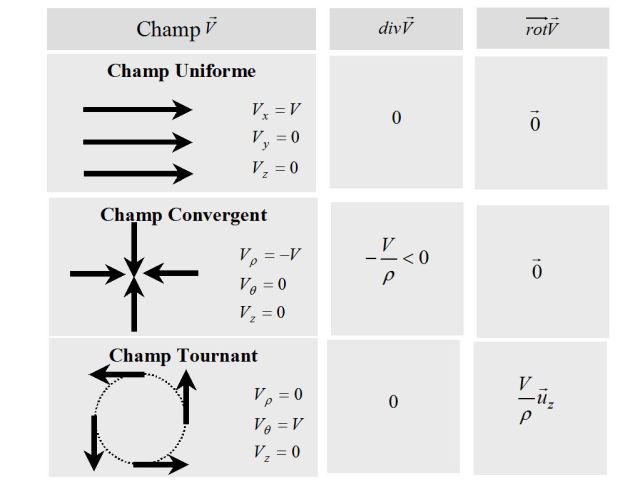
The curl operator of the last field (fields lines rotate around point O in the positf side) is positif.
The considered field can be that of velocity of a solid rotating about the(Oz) axis .
The speed of a point of the solid is, if
 denotes the rotation vector of the solid,,
denotes the rotation vector of the solid,,
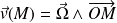 .
.
Using Cartesian coordinates :
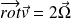
This result allows to associate the curl operator to the idea of rotation.
