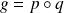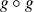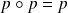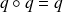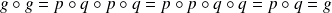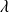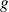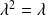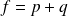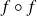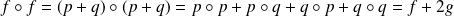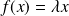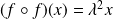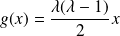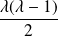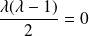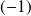Exo 5
Soient
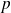et
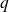deux projecteurs d'un espace vectoriel
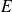de dimension finie.
On suppose que
.
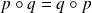Question
Question
Question
Démontrer que
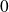est valeur propre de
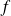si et seulement si
.
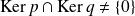Démontrez les deux implications.
On suppose que
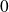est valeur propre de
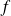. Soit
un vecteur propre associé.Donc :
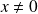et
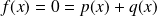. Donc :
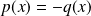.Donc :
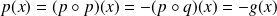.De même :
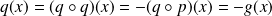.Or :
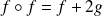. Donc
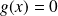. Donc :
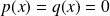.Donc :
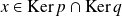. Donc :
.
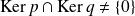Réciproquement, on suppose que
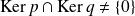.Donc il existe
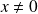tel que
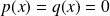. Donc :
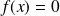.Donc
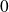est valeur propre de
.
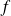Conclusion :
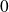est valeur propre de
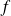si et seulement si
.
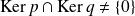Question
Démontrer que
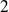est valeur propre de
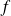si et seulement si
.
Démontrez les deux implications.
On suppose que
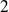est valeur propre de
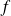. Soit
un vecteur propre associé.Donc :
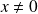et
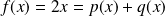. Donc :
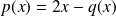.Donc :
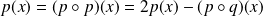. Donc :
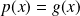.De même :
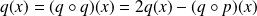. Donc :
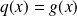.Donc
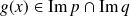. Or :
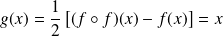. Donc :
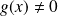.Donc :
.
Réciproquement, on suppose que
. Soit
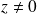appartenant à
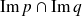.Donc il existe
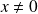et
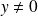tels que
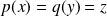.Donc :
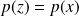et
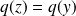. Donc :
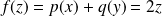.Donc
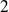est valeur propre de
.
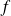Conclusion :
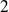est valeur propre de
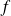si et seulement si
.
