Exo 2
Pour tout
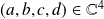, on définit la matrice :
.
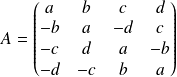Question
Calculer la matrice
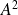et en déduire un polynôme annulateur de
.
.
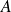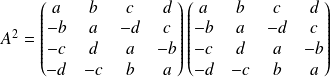Donc :
.
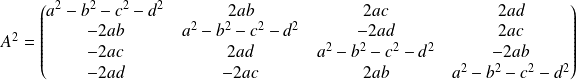Donc :
.
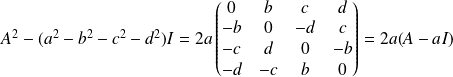Donc :
.
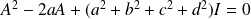Conclusion : Le polynôme
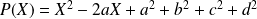est annulateur de
.
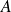Question
En déduire la réduction de la matrice
.
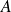Diagonalisez la matrice
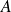ou, si ce n'est pas possible, déterminez une matrice triangulaire semblable à la matrice
.
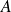On remarque que :
.
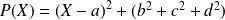Il existe
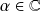tel que :
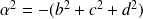. Donc :
.
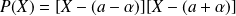Donc :
.
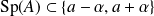Supposons
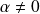. Le polynôme annulateur
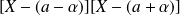est scindé à racines simples. Donc
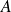est diagonalisable.Et
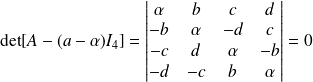car les colonnes sont liées :
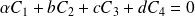.Et de même
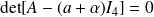en remplaçant
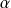par
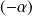.Donc :
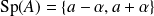. Donc le polynôme caractéristique de
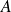a pour racines
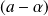et
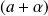. Or
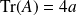, donc les deux racines ont le même ordre de multiplicité, donc
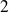.Conclusion : Si
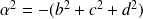et
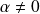, la matrice
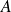est semblable à la matrice
.
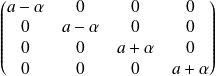Supposons
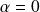. Donc
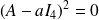, donc
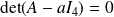, et donc
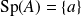.Donc
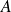est diagonalisable si et seulement si
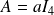, donc si
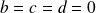.Conclusion : Si
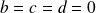, alors
.
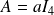Supposons
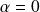et
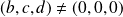. Donc
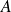n'est pas diagonalisable. Soit
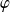l'endomorphisme de matrice
.
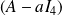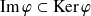car
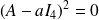. Donc, d'après le théorème du rang :
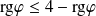, donc
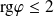. Or
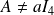, donc
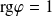ou
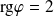.Si
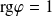, les vecteurs colonnes de
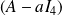seraient colinéaires, donc on aurait
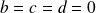, ce qui est exclu. Donc
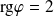et
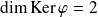. Donc
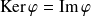.Soit
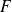un sous-espace vectoriel supplémentaire de
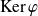. Il est donc de dimension
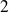. Soit
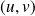une base de
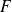, et soient
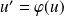et
.
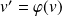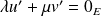si et seulement si
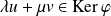. Or
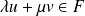.Donc
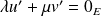si et seulement si
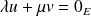, donc si
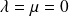car
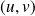est libre.Donc
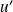et
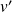forment une famille libre, donc une base de
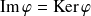.Donc
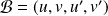est une base de
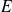et la matrice de
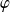dans
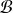est
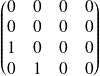.Conclusion : Si
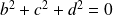et
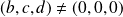, la matrice
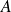est semblable à
.
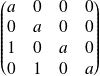