Exo 1
Soit
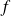l'endomorphisme de
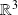de matrice
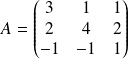dans la base canonique.
Question
Déterminer les valeurs propres de
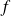et les sous-espaces propres associés.
Déterminez les réels
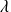tels que l'équation vectorielle
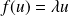ait au moins une solution
.
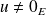Soit
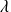une valeur propre de
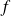et
un vecteur propre associé à
.
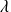Donc
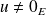et
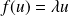, donc :
.
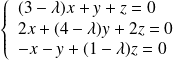Or si le déterminant du système est non nul, le système a pour unique solution
.
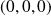Donc pour que
soit vecteur propre de
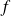associé à
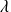, il faut que le déterminant du système soit nul.
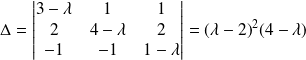. Donc
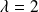ou
.
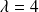Si
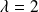, le système devient :
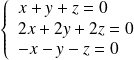, ce qui équivaut à
.
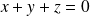Si
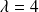, le système devient :
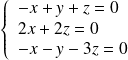, ce qui équivaut à
.
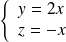Conclusion : Les valeurs propres de
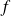sont
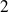et
.
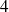Le sous espace propre associé à
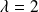est le plan vectoriel d'équation
.
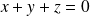Le sous espace propre associé à
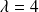est la droite vectorielle de base
.
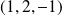