Exo 5
Les questions sont indépendantes.
Question
Etudier la convergence de la série de terme général :
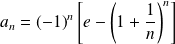 .
.
Montrez que la série est alternée.
A priori, ce n'est pas une série à termes positifs : on étudie le signe de
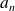 .
.
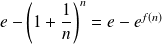 où
où
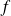 est la fonction définie par :
est la fonction définie par :
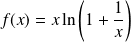 .
.
Cette fonction est de classe
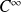 sur
sur
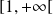 et
et
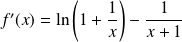 .
.
Donc :
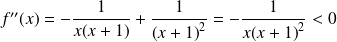 , et donc
, et donc
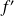 est décroissante sur
est décroissante sur
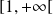 .
.
Or :
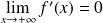 . Donc :
. Donc :
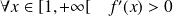 , et donc
, et donc
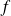 est croissante sur
est croissante sur
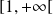 .
.
Or :
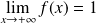 car
car
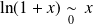 . Donc :
. Donc :
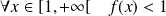 .
.
Donc :
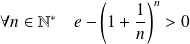 , et donc la série est alternée.
, et donc la série est alternée.
De plus, la suite
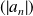 est décroissante car
est décroissante car
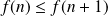 , donc :
, donc :
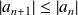 .
.
Et la suite
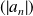 converge vers 0 car
converge vers 0 car
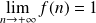 .
.
On applique le critère des séries alternées.
Conclusion : La série
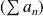 est convergente.
est convergente.
Question
Etudier la convergence de la série de terme général :
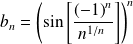 .
.
Etudiez la série
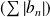 .
.
La série
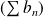 n'est pas à termes positifs.
n'est pas à termes positifs.
On étudie la série
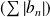 et on utilise le critère de Cauchy.
et on utilise le critère de Cauchy.
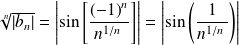 . Or :
. Or :
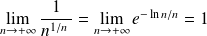 .
.
Donc, par continuité de la fonction sinus :
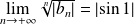 .
.
Or
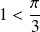 , donc :
, donc :
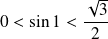 . Donc :
. Donc :
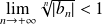 .
.
Donc la série
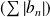 est convergente et la série
est convergente et la série
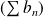 est absolument convergente.
est absolument convergente.
Conclusion : La série
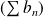 est convergente.
est convergente.
Question
Etudier la convergence de la série de terme général :
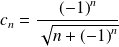 pour
pour
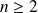 .
.
Etudiez la suite des sommes partielles.
La série
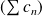 n'est pas une série à termes positifs. Donc on étudie la série
n'est pas une série à termes positifs. Donc on étudie la série
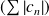 .
.
Or :
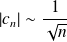 . Donc la série
. Donc la série
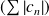 est de même nature que la série
est de même nature que la série
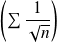 qui est une série de Riemann divergente (
qui est une série de Riemann divergente (
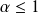 ).
).
Donc la série
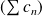 n'est pas absolument convergente.
n'est pas absolument convergente.
Etudions les sommes partielles :
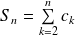 .
.
Donc :
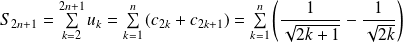 .
.
Et :
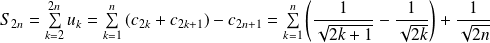 .
.
Soit :
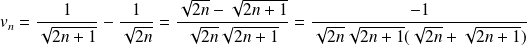 .
.
Donc :
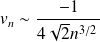 . Donc la série à termes négatifs
. Donc la série à termes négatifs
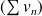 est de même nature que la série
est de même nature que la série
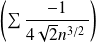 .
.
Or la série
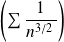 est une série de Riemann convergente car
est une série de Riemann convergente car
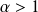 .
.
Donc la série
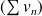 est convergente. Soit
est convergente. Soit
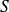 la somme de cette série.
la somme de cette série.
Donc :
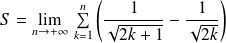 . Donc :
. Donc :
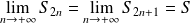 .
.
Donc la suite
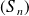 des sommes partielles de la série
des sommes partielles de la série
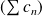 converge.
converge.
Conclusion : La série
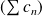 est (semi) convergente.
est (semi) convergente.
Remarque :
La série est alternée, mais on ne peut pas utiliser le critère des séries alternées car
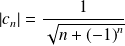 tend vers
tend vers
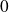 , mais la suite
, mais la suite
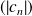 n'est pas décroissante.
n'est pas décroissante.
En effet :
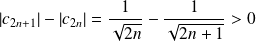 et
et
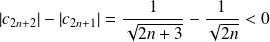 .
.





