Séries entières
Définition :
Une série entière est une série de fonctions de
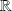 ou
ou
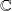 dans
dans
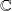 et de la forme
et de la forme
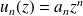 où où
où où
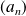 est une suite numérique.
est une suite numérique.
Lemme d'Abel : S'il existe
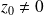 tel que la suite
tel que la suite
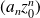 soit bornée, alors la série
soit bornée, alors la série
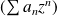 converge absolument pour tout
converge absolument pour tout
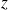 tel que
tel que
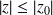 .
.
L'ensemble des réels
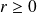 tels que la suite
tels que la suite
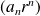 soit bornée est une partie non vide de
soit bornée est une partie non vide de
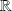 car il contient
car il contient
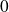 .
.
Définition :
Le rayon de convergence d'une série entière
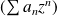 est :
est :
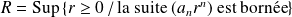 si cet ensemble est majoré.
si cet ensemble est majoré.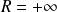 si cet ensemble n'est pas majoré.
si cet ensemble n'est pas majoré.
Le disque de convergence de la série est :
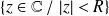 si
si
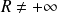 . Sinon, c'est
. Sinon, c'est
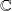 .
.
L'intervalle de convergence de la série est l'intervalle réel
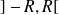 si
si
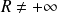 . Sinon, c'est
. Sinon, c'est
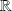 .
.
Le rayon de convergence est aussi :
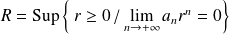 .
.
Fondamental :
Convergence de la série :
Si
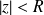 , la série
, la série
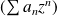 est absolument convergente.
est absolument convergente.Si
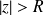 , la série
, la série
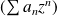 est grossièrement divergente.
est grossièrement divergente.Une série entière est normalement convergente dans tout compact contenu dans son disque de convergence.
Inversement :
Si
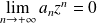 , alors
, alors
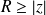 .
. Si la suite
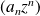 diverge, alors
diverge, alors
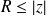 .
.
Les règles de D'Alembert et de Cauchy permettent dans certains cas un calcul pratique du rayon de convergence.
Fondamental :
Règle de D'Alembert :
Soit
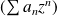 une série entière telle que la suite
une série entière telle que la suite
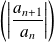 admette une limite
admette une limite
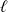 (réelle ou infinie).
(réelle ou infinie).
Si
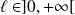 , alors :
, alors :
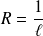 .
.Si
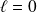 , alors :
, alors :
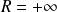 .
.Si
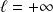 , alors :
, alors :
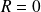 .
.
Règle de Cauchy :
Soit
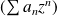 une série entière telle que la suite
une série entière telle que la suite
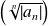 admette une limite
admette une limite
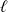 (réelle ou infinie).
(réelle ou infinie).
Si
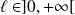 , alors :
, alors :
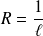 .
.Si
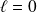 , alors :
, alors :
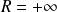 .
.Si
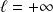 , alors :
, alors :
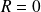 .
.
La comparaison des coefficients de deux séries entières permet de comparer leurs rayons de convergence.
Fondamental :
Comparaison de séries entières
Soient
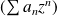 et
et
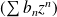 deux séries entières de rayons de convergence
deux séries entières de rayons de convergence
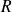 et
et
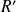 .
.
Si
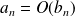 ou
ou
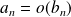 , alors :
, alors :
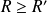 .
. Si
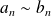 , alors :
, alors :
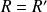 .
.
Fondamental :
Somme de deux séries entières
Si les séries entières
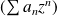 et
et
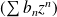 ont pour rayon de convergence
ont pour rayon de convergence
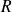 et
et
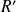 , alors la série
, alors la série
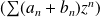 a un rayon de convergence
a un rayon de convergence
 avec égalité si
avec égalité si
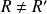 .
.
Et si
 , alors :
, alors :
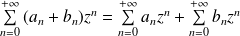 .
.
Fondamental :
Produit de Cauchy de deux séries entières
Le produit de Cauchy des séries entières
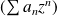 et
et
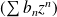 est la série entière
est la série entière
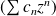 avec
avec
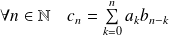 .
.
Si les séries entières
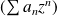 et
et
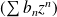 ont pour rayon de convergence
ont pour rayon de convergence
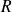 et
et
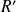 , alors leur produit de Cauchy
, alors leur produit de Cauchy
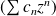 a un rayon de convergence
a un rayon de convergence
 .
.
Si
 , alors :
, alors :
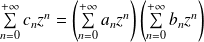 .
.





