Convergence d'une suite de fonctions
Les fonctions sont définies sur un intervalle
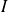de
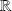à valeurs réelles ou complexes.
Définition :
Convergence simple (ou ponctuelle)
La suite de fonctions
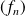converge simplement sur
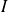vers la fonction
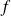si :
.
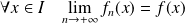Cela se traduit par :
.
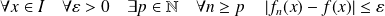Exemple :
Exemple : On considère la suite de fonctions définies sur
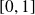par
.
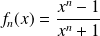Cette suite converge simplement vers la fonction
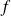définie par
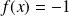si
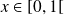et
.
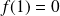Sur cet exemple, on peut remarquer que la continuité des fonctions
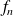n'entraîne pas la continuité de la limite
.
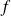Il faut une notion de convergence plus forte.
Rappel : Si une fonction
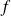est bornée sur un intervalle
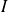, on note
.
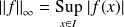Définition :
Convergence uniforme
La suite de fonctions
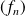converge uniformément sur
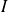vers la fonction
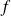si
.
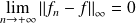Cela se traduit par :
.
A partir d'un certain rang, les fonctions
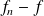doivent être bornées.
Exemple :
Exemple : On considère la suite de fonctions définies sur
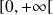par
.
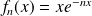Après avoir étudié la convergence simple, montrer que la convergence est uniforme. Solution
Dans le cas de la convergence simple, l'entier
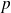dépend de
, alors que dans la convergence uniforme, l'entier
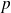est le même pour tous les
.
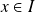Fondamental :
La convergence uniforme entraîne la convergence simple.
Mais, évidemment, la réciproque est fausse.
Fondamental :
S'il existe une suite numérique
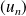convergeant vers
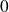telle que
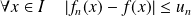, alors la convergence est uniforme.S'il existe une suite
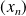de
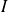telle que
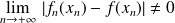, alors la convergence n'est pas uniforme.
Par exemple, la suite
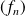définie sur
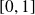par
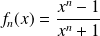converge simplement vers la fonction
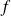définie par
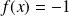si
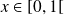et
.
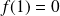Mais la convergence n'est pas uniforme car si
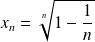, alors
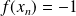et
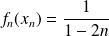tend vers
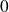, donc
.
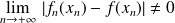Fondamental :
La convergence uniforme sur
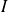entraîne la convergence uniforme locale sur
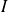, c'est-à-dire sur tout segment inclus dans
.
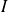Mais la réciproque est fausse.
Par exemple la suite
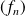définie sur
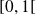par
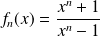converge simplement vers la fonction
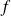définie par
.
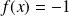La convergence est uniforme sur tout segment
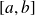inclus dans
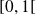car
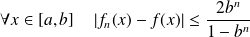qui tend vers
.
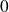Mais la convergence n'est pas uniforme sur
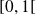car si
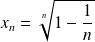, alors
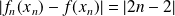, donc ne tend pas vers
.
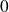