Espaces vectoriels de dimension finie
Définition :
Si un espace vectoriel
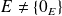a une famille génératrice finie, il possède au moins une base et toutes ses bases ont le même nombre
de vecteurs.
Ce nombre
s'appelle la dimension de
:
.
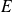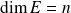Et par convention :
.
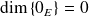Exemple :
Exemples classiques
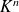est un espace vectoriel de dimension finie et
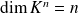. Sa base canonique est :
,
, ...,
.
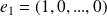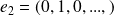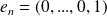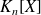est un espace vectoriel de dimension finie et
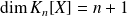. Sa base canonique est
. 
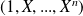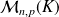est un espace vectoriel de dimension finie et
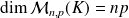.Sa base canonique est formée par les matrices
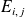dont tous les termes sont nuls sauf le terme de la
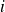ème ligne et de la
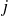ème colonne qui vaut
.
Par contre, par exemple, l'espace vectoriel
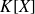des polynômes sur
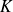n'est pas de dimension finie.
Fondamental :
Propriétés des familles de vecteurs dans un espace vectoriel
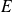de dimension
:
Toute base de
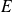a
vecteurs.Toute famille libre de
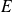a au plus
vecteurs.Toute famille génératrice de
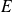a au moins
vecteurs.Toute famille libre de
vecteurs de
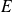est une base de
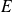.Toute famille génératrice de
vecteurs de
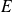est une base de
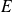.Toute famille libre de
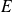peut être complétée en une base de
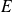(Théorème de la base incomplète)De toute famille génératrice de
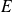, on peut extraire une base de
.
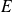Fondamental :
Propriétés des sous-espaces vectoriels dans un espace vectoriel
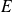de dimension finie :
Si
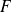est un sous-espace vectoriel de
:
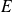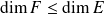(Il y a égalité si et seulement si
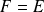).Si
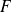et
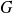sont des sous-espaces vectoriels de
:
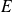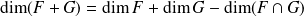.Deux sous-espaces
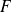et
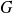sont supplémentaires si et seulement si :
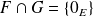et
.
Définition :
Le rang d'une famille de vecteurs
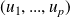est :
.
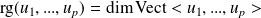