Sous-espaces vectoriels
Dans ce qui suit,
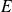 désigne un
désigne un
 - espace vectoriel.
- espace vectoriel.
Définition :
Une partie
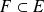 est un sous-espace vectoriel de
est un sous-espace vectoriel de
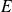 si la restriction des lois à
si la restriction des lois à
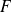 munit
munit
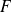 d'une structure d'espace vectoriel.
d'une structure d'espace vectoriel.
Une partie
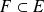 est un sous-espace vectoriel de
est un sous-espace vectoriel de
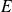 si et seulement si
si et seulement si
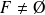 et :
et :
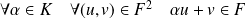 .
.
Fondamental :
Propriétés :
Tout sous-espace vectoriel de
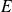 contient
contient
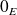 .
.Tout sous-espace vectoriel de
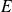 est stable par combinaison linéaire : pour tous les vecteurs
est stable par combinaison linéaire : pour tous les vecteurs
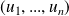 de
de
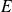 et tous les scalaires
et tous les scalaires
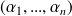 , le vecteur
, le vecteur
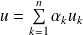 appartient à
appartient à
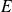 .
.Si
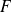 et
et
 sont des sous-espaces vectoriels de
sont des sous-espaces vectoriels de
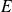 , alors
, alors
 est un sous-espace vectoriel de
est un sous-espace vectoriel de
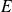 .
.
Par contre, la réunion de deux sous-espaces vectoriels n'est en général pas un sous-espace vectoriel.
Définition :
La somme de deux sous-espaces vectoriels
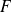 et
et
 de
de
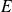 est :
est :
 .
.
C'est le plus petit sous-espace vectoriel de
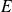 contenant
contenant
 .
.
Définition :
Si
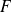 et
et
 sont des sous-espaces vectoriels de
sont des sous-espaces vectoriels de
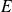 , la somme
, la somme
 est directe si
est directe si
 . On la note
. On la note
 .
.
Une somme
 est directe si et seulement si tout vecteur de
est directe si et seulement si tout vecteur de
 se décompose de manière unique en
se décompose de manière unique en
 où
où
 et
et
 .
.
Définition :
Deux sous-espaces vectoriels
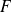 et
et
 sont supplémentaires si
sont supplémentaires si
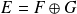 .
.
Deux sous-espaces
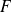 et
et
 sont supplémentaires si et seulement si :
sont supplémentaires si et seulement si :
 .
.
Exemples :
L'ensemble
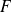 des applications paires et l'ensemble
des applications paires et l'ensemble
 des applications impaires de
des applications impaires de
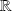 dans
dans
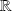 sont deux sous-espaces vectoriels supplémentaires dans l'espace vectoriel
sont deux sous-espaces vectoriels supplémentaires dans l'espace vectoriel
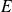 des applications de
des applications de
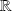 dans
dans
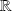 .
.En effet, toute application
 peut s'écrire
peut s'écrire
 avec
avec
 et
et
 .
.Et cette décomposition de
 en somme d'une application paire et d'une application impaire est unique.
en somme d'une application paire et d'une application impaire est unique.L'ensemble
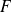 des matrices symétriques et l'ensemble
des matrices symétriques et l'ensemble
 des matrices antisymétriques sont deux sous-espaces vectoriels supplémentaires dans l'espace vectoriel
des matrices antisymétriques sont deux sous-espaces vectoriels supplémentaires dans l'espace vectoriel
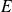 des matrices carrées d'ordre
des matrices carrées d'ordre
 .
.En effet, toute matrice
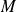 peut s'écrire
peut s'écrire
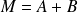 avec
avec
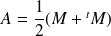 et
et
 .
.Et cette décomposition de
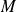 en somme d'une matrice symétrique et d'une matrice antisymétrique est unique.
en somme d'une matrice symétrique et d'une matrice antisymétrique est unique.
Définition :
Si
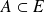 on appelle sous-espace vectoriel engendré par
on appelle sous-espace vectoriel engendré par
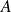 le plus petit sous-espace vectoriel contenant
le plus petit sous-espace vectoriel contenant
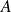 .
.
On le note
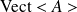 ou
ou
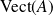 .
.
Le sous-espace engendré par
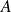 est l'intersection de tous les sous-espaces vectoriels qui contiennent
est l'intersection de tous les sous-espaces vectoriels qui contiennent
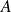 .
.
Le sous-espace engendré par
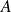 est l'ensemble des combinaisons linéaires des vecteurs de
est l'ensemble des combinaisons linéaires des vecteurs de
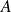 .
.
En particulier :
 .
.





