Familles de vecteurs
Dans ce qui suit,
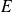désigne un
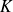- espace vectoriel.
Définition :
Une famille
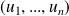de vecteurs d'un sous-espace vectoriel
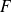est une famille génératrice de
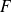si
.
C'est équivalent à dire que :
.
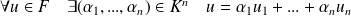Fondamental :
Propriétés :
Toute famille de vecteurs de
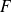qui contient une famille génératrice de
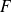est génératrice de
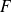.Si l'un des vecteurs d'une famille génératrice de
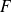est combinaison linéaire des autres, la famille privée de ce vecteur est génératrice de
.
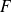Définition :
Une famille
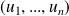de vecteurs de
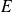est une famille libre si :
.
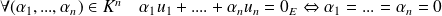Fondamental :
Propriétés :
La famille
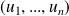est libre si et seulement si tout vecteur de
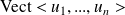s'écrit de manière unique comme combinaison linéaire de
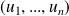.Toute famille extraite d'une famille libre est libre.
La famille
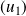est libre si et seulement si
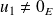. La famille
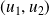est libre si et seulement si
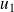et
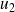ne sont pas colinéaires.
Définition :
Une famille
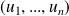de vecteurs de
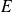est une famille liée si elle n'est pas libre, donc si :
.
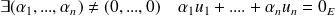Fondamental :
Propriétés :
La famille est liée si et seulement si l'un des vecteurs est combinaison linéaire des autres.
Toute famille qui contient une famille liée est liée.
Définition :
Une famille
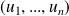de vecteurs d'un sous-espace vectoriel
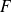est une base de
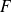si elle est libre et génératrice de
.
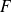Une famille
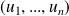de vecteurs de
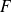est une base de
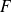si et seulement si :
.
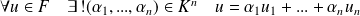Les coefficients
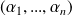sont les coordonnées de
dans la base
.
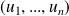