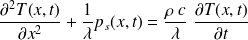Équation de la diffusion de la chaleur
Rappel : Équation de la chaleur ou de la diffusion thermique à une dimension (sans ou avec sources)
En utilisant la loi de Fourier :
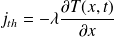
Il vient :
Équation de la chaleur sans sources :
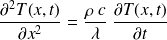
Équation de la chaleur avec sources :
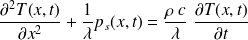
Il n'existe de solutions analytiques de cette équation que dans des cas particuliers que l'on étudiera dans les paragraphes suivants.
La solution de cette équation aux dérivées partielles dépend de constantes d'intégration qui sont déterminées par les conditions aux limites spatiales et temporelles.
Si ces conditions traduisent toutes les données significatives du problème physique, la solution obtenue est unique et c'est donc la bonne !
Attention : Équation de la chaleur ou de la diffusion thermique à une dimension
En l'absence de sources :
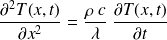
En présence de sources :