Réaliser des mesures d'optique avec un Michelson
Quelques vidéos d'illustration sur le Michelson
Présentation du Michelson par le MIT
Réglages du Michelson au Laser
Méthode : Réalisation d'un spectre cannelé
Obtenir les teintes de Newton puis charioter légèrement afin d'observer le blanc d'ordre supérieur.
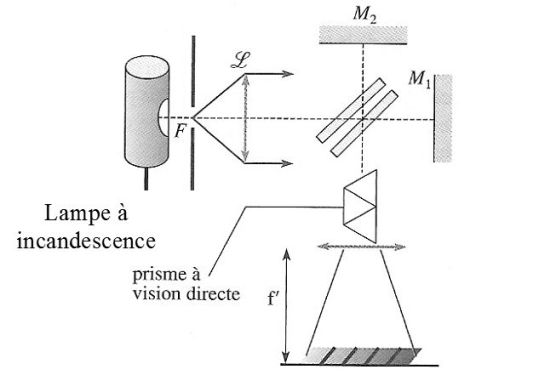
Faire l'image d'une fente verticale placée juste contre la lampe sur l'écran d'observation à l'aide d'une lentille de focale 10 cm.
En intercalant un prisme à vision directe à la sortie de l'interféromètre, on observe la décomposition spectrale de la lumière sous la forme d'un spectre cannelé.
On peut également placé l'œil directement à la sortie du prisme à vision directe.
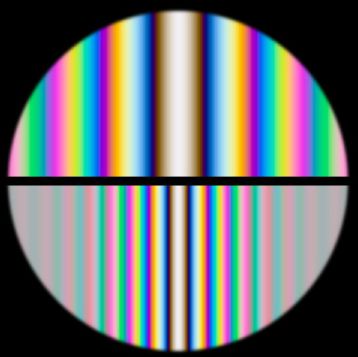
Un beau spectre cannelé !
Méthode : Étude de l'épaisseur optique d'une lame de mica mince
Le mica est le nom d'une famille de minéraux, du groupe des silicates sous-groupe des phyllosilicates formé principalement de silicate d'aluminium et de potassium. Avec le quartz et le feldspath, il est l'un des constituants du granite.
Obtenir de nouveau les teintes de Newton et placer la frange centrale au milieu de l'écran d'observation.
Noter la graduation x1 donnée par le vernier.
Introduire entre la séparatrice et le miroir (M1) une lame de mica transparente de faible épaisseur e.
Les franges disparaissent car le chemin optique a été rallongé sur cette voie de
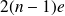. On prendra n = 1,58 pour l'indice de la lame de mica.
Charioter lentement afin de retrouver les franges et noter la nouvelle valeur x2 du vernier.
On peut en déduire l'épaisseur de la lame par :
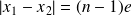
Remarque : il n'est pas toujours facile de retrouver la teinte sensible ; en cas de soucis, il peut-être bon d'utiliser un filtre interférentiel et la méthode vue lors du réglage de l'interféromètre.
Méthode : Étude du doublet jaune du sodium
La lampe au sodium émet deux raies de longueur d'onde
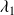et
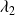très proches l'une de l'autre :
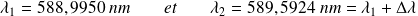
On souhaite mesurer cet écart
.
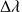Se placer en configuration "lame d'air" avec une lampe à vapeur de sodium.
Régler l'écart e entre les deux miroirs pour voir peu d'anneaux (on est proche du contact optique).
Translater le miroir dans le sens où les anneaux naissent au centre.
Vérifier que le contraste varie ; il s'annule périodiquement.
Lire les différentes valeurs des positions de (M1) pour lesquelles le contraste est minimal (anticoïncidence).
Démontrer que, pour une différence de marche
évaluée pour un angle d'incidence
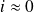et pour une épaisseur de lame d'air égale à e, l'éclairement résultant de la présence de deux longueurs d'ondes dans la lampe spectrale à vapeur de sodium est :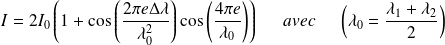 
En déduire la largeur
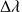du doublet par la relation :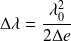
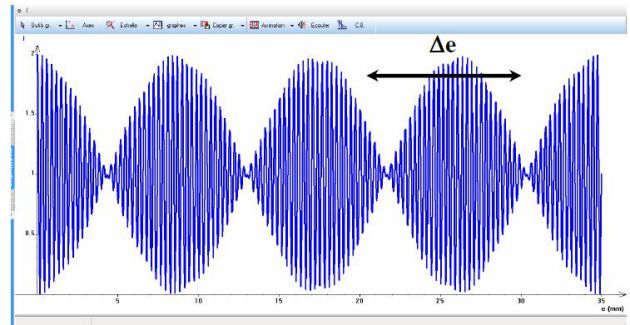
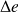étant la distance entre deux positions successives de (M1) pour lesquelles le contraste est minimal.Pour augmenter la précision, il faut bien sûr prendre le maximum de positions de (M1) pour lesquelles le contraste est minimal.
Méthode : Mesure de l'angle alpha pour le coin d'air
Projeter une dizaine de franges du coin d'air avec la lampe à sodium.
Mesurer l'interfrange sur l'écran.
Quel est le grandissement sur l'écran donné par la lentille de projection ?
En déduire l'interfrange réel sur la surface des miroirs et en déduire l'ordre de grandeur de l'angle
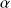du coin d'air.
Méthode : Mesure de la largeur spectrale d'un filtre interférentiel
Obtenir les teintes de Newton (montage du coin d'air).
Placer la frange centrale au milieu de l'écran et vérifier la position du vernier.
Placer un filtre interférentiel (vert par exemple) après la lampe à incandescence.
Translater le miroir (M1) et vérifier que le contraste diminue et finit par s'annuler.
Noter la position
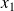du miroir (M1).Translater le miroir (M1) en sens contraire jusqu'à obtenir de nouveau un contraste nul.
Noter la position
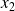du miroir (M1).
À la disparition des franges, l'écart entre les deux miroirs est
.
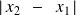La longueur moyenne des trains d'onde est donc
.
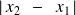On sait que la largeur spectrale
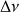de la lumière que laisse passer le filtre vaut :
(
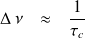
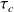étant la durée moyenne des trains d'onde)
La longueur moyenne des trains d'onde ou longueur de cohérence temporelle
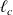est reliée à la durée moyenne des trains d'onde par :
(c : vitesse de la lumière dans le vide)
En déduire la largeur spectrale
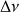du filtre.
Autre mesure : mesure de la largeur spectrale d'une raie quasi – monochromatique (la raie verte du mercure)
Placer le filtre interférentiel vert devant la lampe à mercure et se placer en coin d'air.
La largeur de la raie verte du mercure est beaucoup plus étroite que la bande passante du filtre dont le seul rôle est d'éliminer les autres raies sans modifier la raie verte.
Procéder comme précédemment pour obtenir la longueur de cohérence de la raie verte du mercure.
Ordre de grandeur :
Pour la raie verte du mercure,
.
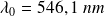La longueur de cohérence (pour une lampe à haute pression) est
.
Par conséquent :
Et :
