Oscillateur à pont de Wien
Exemple : Oscillateur à pont de Wien
Une vidéo sur l'oscillateur à pont de Wien
Méthode : Filtre passe-bande
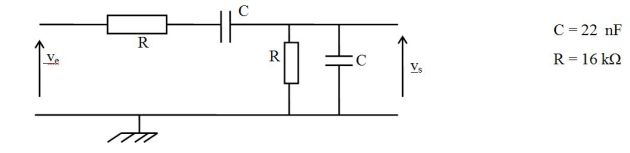
La fonction de transfert du circuit suivant (c'est un filtre passe-bande) est :

Avec :
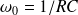 et
et
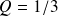 .
.
Expérience :
Réaliser le montage avec les valeurs proposées sur la figure
Vérifier la nature du filtre obtenu
Évaluer expérimentalement
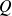 et
et
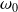 .
. On rappelle que la largeur de la bande passante d'un filtre passe-bande est donnée par :

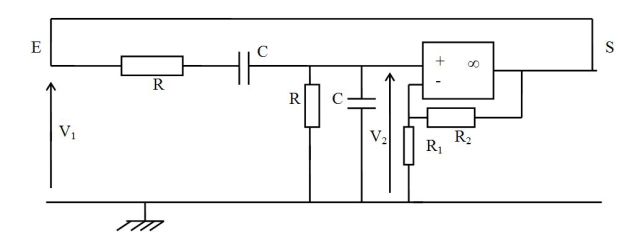
Méthode : Réalisation de l'oscillateur
On réalise le montage de la figure suivante, avec :
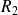 : une résistance de
: une résistance de
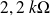
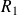 : une série de boîtes de
: une série de boîtes de
 ,
,
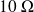 ,
,
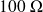 et
et
 .
.Les valeurs de
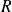 et de
et de
 sont celles données au paragraphe précédent.
sont celles données au paragraphe précédent.
Étude théorique :
Déterminer l'équation différentielle du second ordre vérifiée par
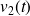 (on posera
(on posera
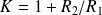 ).
).Calculer la valeur
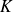 nécessaire pour obtenir des oscillations sinusoïdales.
nécessaire pour obtenir des oscillations sinusoïdales.On choisit
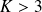 avec
avec
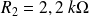 .
.Justifier que la tension
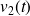 peut s'écrire :
peut s'écrire : 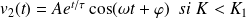
Donner la valeur de
 . Exprimer
. Exprimer
 et
et
 en fonction de
en fonction de
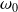 et
et
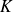 .
.Calculer
 et
et
 pour
pour
 .
.Que donne le résultat mathématique concernant l'amplitude des oscillations si
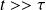 ?
? Que se passe-t-il réellement ?
Comment évoluerait l'amplitude des oscillations pour
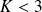 ?
?
Étude expérimentale :
Réaliser le montage :
Quel problème se pose pour l'obtention d'oscillations sinusoïdales pures ?
Mesurer la valeur de la pulsation du signal lorsque celui-ci est accroché.
La comparer avec celle qui assure le maximum du gain pour le pont de Wien.
Stabilisation en amplitude des oscillations sinusoïdales :
On reprend le montage précédent en supposant que des oscillations sinusoïdales de pulsation
 et d'amplitudes
et d'amplitudes
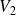 pour
pour
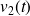 et
et
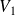 pour
pour
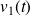 apparaissent.
apparaissent. On se propose de stabiliser les oscillations en prenant pour
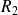 une thermistance à coefficient de température négatif (CTN) suivant la loi :
une thermistance à coefficient de température négatif (CTN) suivant la loi : 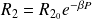
où
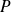 est la puissance électrique moyenne dissipée dans cet élément et
est la puissance électrique moyenne dissipée dans cet élément et
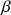 une constante positive.
une constante positive.Remplacer la résistance
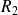 par la CTN qui a ici une valeur de résistance de
par la CTN qui a ici une valeur de résistance de
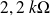 pour une température de 25°C.
pour une température de 25°C. Sa valeur augmente si la température décroît, et réciproquement.
Expliquer pourquoi ce dispositif permet de stabiliser les oscillations.
Faire varier
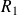 pour trouver les limites d'accrochage et de saturation du signal.
pour trouver les limites d'accrochage et de saturation du signal.