Bobine en mouvement dans un solénoïde
Consacrer 15 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Une bobine plate est constituée de N = 1 000 tours de fils enroulés sur un support circulaire de centre O et de rayon a = 0,1 m.
Cette bobine est mise en rotation à vitesse angulaire ω autour de l'axe Oy au moyen d'un moteur électrique.
La bobine est fermée sur elle même et placée dans un champ magnétique uniforme
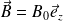, avec
.
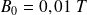La tension d'alimentation du moteur est
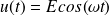et à t = 0, la normale à la bobine
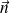est confondue avec
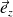. u(t) est de fréquence 50 Hz.
A un instant quelconque t la vue en coupe est donc la suivante :
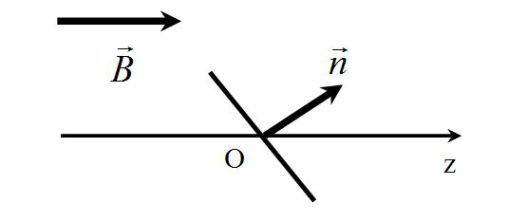
On mesure l'intensité dans la bobine au moyen d'un multimètre utilisé en position AC dans la gamme 2 A.
L'indication est 1,54 A.
A l'oscilloscope on observe u(t) ainsi qu'une tension proportionnelle au courant i(t) passant dans la bobine.
Question
Pourquoi existe-t-il un courant dans la bobine ?
Déterminer l'équation différentielle vérifiée par i(t).
C'est le principe d'une dynamo de vélo !
Penser à la loi de Faraday
Il y a un courant par l'effet de la fem induite (flux variable). On obtient :
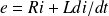
Avec : (loi de Faraday)
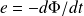
Où :
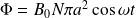
D'où :
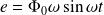
Avec :
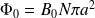
Question
À partir des résultats expérimentaux, calculer la résistance et l'inductance de la bobine.
La solution en régime forcé est :
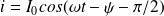
Avec : (se placer en notation complexe)
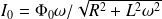
Et :
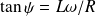
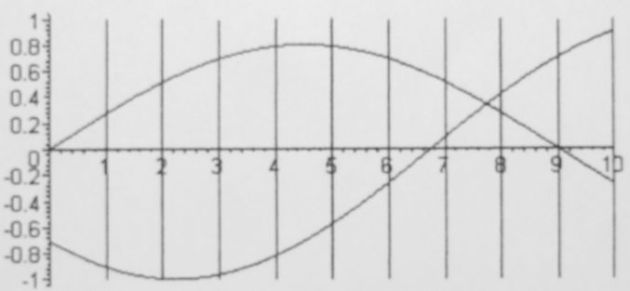
i(t) est donc en retard par rapport à u(t). On mesure un déphasage de 6,75 carreaux, soit -135°, donc :
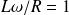
Ainsi :
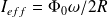
On trouve :
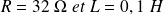
Question
La bobine maintenant alimentée par un générateur continu de fem E = 10 V est placée au centre d'un solénoïde très long caractérisé par n = 100 spires par mètre (le champ B0 est supprimé).
De même que précédemment, la bobine est en rotation autour de l'axe Oy.
Calculer la tension qui apparaît aux bornes de la bobine.
La bobine est parcourue par :
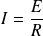
Pour déterminer le flux à travers le solénoïde on utilise le coefficient de mutuelle M.
Si i0 est le courant dans le solénoïde, le flux dans le bobine est
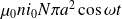. Donc :
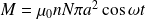
Le flux à travers le solénoïde devient
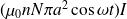et la fém induite est :
