Fonctions numériques de plusieurs variables
Soit
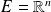 (ou un espace vectoriel normé de dimension
(ou un espace vectoriel normé de dimension
 sur
sur
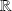 ), et
), et
 une fonction de
une fonction de
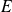 dans
dans
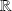 .
.
Définition :
Une fonction
 définie sur un ouvert
définie sur un ouvert
 non vide de
non vide de
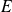 est continue en un point
est continue en un point
 de
de
 si :
si :
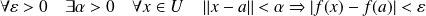 .
.
Une fonction
 définie sur un ouvert
définie sur un ouvert
 non vide de
non vide de
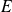 est continue sur
est continue sur
 si elle est continue en tout point de
si elle est continue en tout point de
 .
.
Exemple :
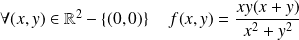 et
et
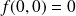 .
.
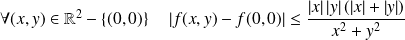 .
.
Or :
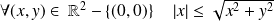 et
et
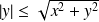 .
.
Donc :
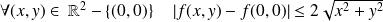 .
.
Donc la fonction
 est continue en
est continue en
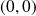 car :
car :
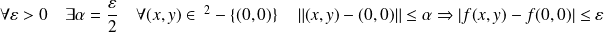 .
.
Fondamental :
Opérations algébriques
Si
 et
et
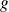 sont deux fonctions définies sur un ouvert
sont deux fonctions définies sur un ouvert
 non vide de
non vide de
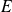 et si elles sont continues en un point
et si elles sont continues en un point
 de
de
 , alors :
, alors :
leur somme
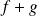 est continue en
est continue en
 .
.leur produit
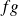 est continue en
est continue en
 .
.leur quotient
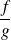 est continue en
est continue en
 à condition que
à condition que
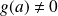 .
.
Exemple :
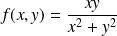 si
si
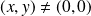 , et :
, et :
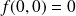 .
.
Les fonctions
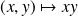 et
et
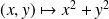 sont polynômiales, donc continues sur
sont polynômiales, donc continues sur
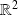 .
.
Donc, par quotient, la fonction
 est continue sur
est continue sur
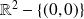 .
.
Fondamental :
Composition
Si
 est une fonction définie sur un ouvert
est une fonction définie sur un ouvert
 non vide de
non vide de
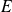 et continue en un point
et continue en un point
 de
de
 , et si
, et si
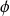 est une fonction définie sur
est une fonction définie sur
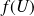 et continue en
et continue en
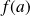 , alors la fonction
, alors la fonction
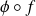 est continue en
est continue en
 .
.Si
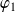 , ...,
, ...,
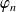 sont des fonctions définies sur une partie
sont des fonctions définies sur une partie
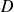 de
de
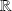 et continues en
et continues en
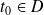 , et si
, et si
 est une fonction définie sur un ouvert
est une fonction définie sur un ouvert
 contenant
contenant
 et continue en
et continue en
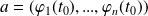 , alors la fonction
, alors la fonction
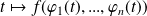 est continue en
est continue en
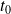 .
.
Dans l'exemple précédent, si
 était continue en
était continue en
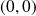 , on aurait :
, on aurait :
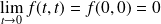 .
.
Or :
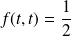 si
si
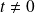 . Donc la fonction
. Donc la fonction
 n'est pas continue en
n'est pas continue en
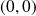 .
.
Définition :
La fonction
 admet un développement limité d'ordre
admet un développement limité d'ordre
 en
en
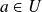 s'il existe une application linéaire
s'il existe une application linéaire
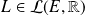 et un voisinage
et un voisinage
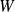 de
de
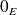 tels que :
tels que :
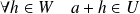 et
et
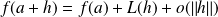 .
.
Si cette application linéaire
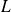 existe, elle est unique. On dira que
existe, elle est unique. On dira que
 est différentiable en
est différentiable en
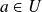 et
et
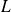 est l'application linéaire tangente de
est l'application linéaire tangente de
 en
en
 .
.
La fonction
 est différentiable sur l'ouvert
est différentiable sur l'ouvert
 si elle est différentiable en tout point de
si elle est différentiable en tout point de
 .
.
Sa différentielle est l'application
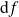 de
de
 dans
dans
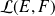 qui à tout point
qui à tout point
 de
de
 associe l'application linéaire tangente de
associe l'application linéaire tangente de
 en
en
 :
:
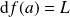 .
.
Exemple :
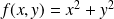 . Donc si
. Donc si
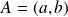 et
et
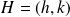 :
:
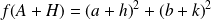 .
.
Donc :
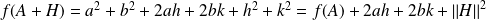 .
.
L'application
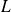 :
:
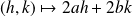 est linéaire de
est linéaire de
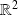 dans
dans
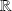 . Et :
. Et :
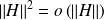 .
.
Donc :
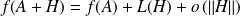 . Donc
. Donc
 est différentiable en tout point de
est différentiable en tout point de
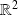 .
.
Sa différentielle
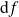 est l'application qui à tout
est l'application qui à tout
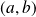 de
de
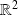 associe l'application linéaire :
associe l'application linéaire :
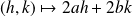 .
.
Fondamental :
Propriétés
Si la fonction
 est différentiable en
est différentiable en
 , alors
, alors
 est continue en
est continue en
 .
.Si
 et
et
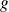 sont différentiables en
sont différentiables en
 , alors
, alors
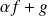 est différentiable en
est différentiable en
 pour tout réel
pour tout réel
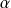 .
.Et :
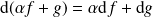 .
.Si
 est différentiable en
est différentiable en
 et si
et si
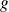 est différentiable en
est différentiable en
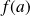 , alors
, alors
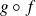 est différentiable en
est différentiable en
 . Et :
. Et :
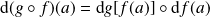 .
.Si
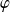 est une fonction de
est une fonction de
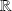 dans
dans
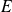 dérivable en
dérivable en
 et si
et si
 est différentiable en
est différentiable en
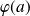 , alors
, alors
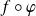 est dérivable en
est dérivable en
 .
. Et :
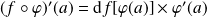 .
.
Définition :
La fonction
 admet une dérivée en
admet une dérivée en
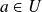 suivant le vecteur
suivant le vecteur
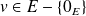 si la fonction
si la fonction
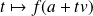 est dérivable en
est dérivable en
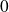 .
.
La dérivée de
 en
en
 suivant le vecteur
suivant le vecteur
 est la fonction définie par :
est la fonction définie par :
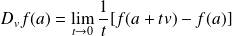 .
.
Exemple : Soit
 la fonction définie par
la fonction définie par
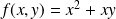 .
.
Soit
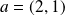 et
et
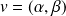 un vecteur non nul.
un vecteur non nul.
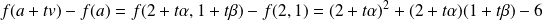 .
.
Donc :
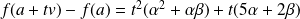 .
.
Donc
 admet en
admet en
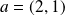 une dérivée suivant
une dérivée suivant
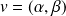 :
:
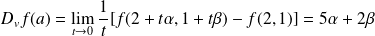 .
.
Fondamental :
Propriété : Si
 est différentiable en
est différentiable en
 , alors
, alors
 admet en
admet en
 une dérivée suivant tous les vecteurs. Et :
une dérivée suivant tous les vecteurs. Et :
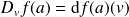 .
.
Définition :
Si
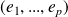 est une base de
est une base de
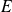 ,
,
 admet une dérivée partielle en
admet une dérivée partielle en
 par rapport à
par rapport à
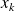 si
si
 admet une dérivée en
admet une dérivée en
 suivant le vecteur
suivant le vecteur
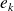 .
.
La dérivée partielle de
 en
en
 par rapport à
par rapport à
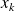 est la fonction définie par :
est la fonction définie par :
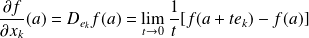 .
.
Méthode :
Dans la pratique, pour calculer la dérivée partielle de
 par rapport à une variable
par rapport à une variable
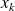 en
en
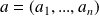 , on considère toutes les autres variables comme des paramètres constants, et on dérive la fonction
, on considère toutes les autres variables comme des paramètres constants, et on dérive la fonction
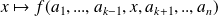 en
en
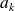 .
.
Dans l'exemple précédent, la dérivée partielle par rapport à
 est la dérivée de la fonction
est la dérivée de la fonction
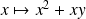 .
.
Donc :
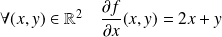 . Donc :
. Donc :
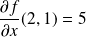 .
.
De même, la dérivée partielle par rapport à
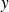 est la dérivée de la fonction
est la dérivée de la fonction
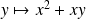 .
.
Donc :
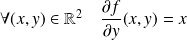 . Donc :
. Donc :
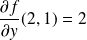 .
.
Fondamental :
Propriétés
Si
 est différentiable en
est différentiable en
 , alors
, alors
 admet des dérivées partielles d'ordre
admet des dérivées partielles d'ordre
 et :
et :
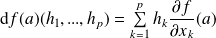 .
.Si
 admet des dérivées partielles continues en
admet des dérivées partielles continues en
 , alors
, alors
 est différentiable en
est différentiable en
 .
.
Attention ! Une fonction peut admettre des dérivées partielles en
 sans être différentiable en
sans être différentiable en
 .
.
Définition :
La fonction
 est continûment différentiable ou de classe
est continûment différentiable ou de classe
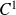 en
en
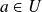 si
si
 est différentiable en
est différentiable en
 et si sa différentielle
et si sa différentielle
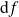 est continue en
est continue en
 .
.
La fonction
 est continûment différentiable ou de classe
est continûment différentiable ou de classe
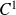 sur
sur
 si
si
 est différentiable sur
est différentiable sur
 et si sa différentielle
et si sa différentielle
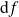 est continue sur
est continue sur
 .
.
Fondamental :
Propriétés
La fonction
 est de classe
est de classe
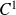 sur
sur
 si et seulement si
si et seulement si
 admet des dérivées partielles sur
admet des dérivées partielles sur
 et si ces dérivées partielles sont continues sur
et si ces dérivées partielles sont continues sur
 .
.Si
 et
et
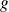 sont de classe
sont de classe
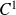 sur
sur
 , alors la fonction
, alors la fonction
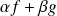 est de classe
est de classe
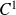 sur
sur
 pour tout
pour tout
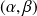 .
.Si
 est de classe
est de classe
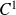 sur
sur
 et si
et si
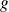 est de classe
est de classe
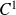 sur un ouvert
sur un ouvert
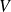 contenant
contenant
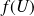 , alors
, alors
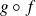 est de classe
est de classe
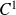 sur
sur
 .
.
Définition :
La fonction
 est de classe
est de classe
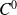 sur un ouvert
sur un ouvert
 non vide si
non vide si
 est continue sur
est continue sur
 .
.
Pour tout
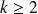 ,
,
 est de classe
est de classe
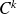 sur
sur
 si
si
 est de classe
est de classe
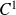 sur
sur
 et si ses dérivées partielles sont de classe
et si ses dérivées partielles sont de classe
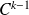 sur
sur
 .
.
Si
 est de classe
est de classe
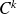 , on définit ses dérivées partielles d'ordre
, on définit ses dérivées partielles d'ordre
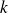 :
:
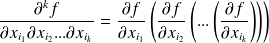 .
.
La fonction
 est de classe
est de classe
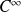 si elle est de classe
si elle est de classe
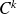 pour tout entier
pour tout entier
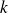 .
.





