Fonction définie par une intégrale
Il s'agit d'étudier la continuité et la dérivabilité de fonctions définies par des intégrales.
On s'intéresse d'abord au cas le plus simple : celui où la variable n'apparaît que dans les bornes.
Rappel :
Si la fonction
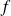est continue par morceaux sur un intervalle
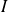de
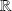et si
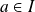, la fonction
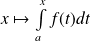est une primitive de
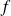sur
.
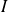Donc la fonction
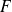définie sur
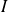par :
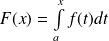est continue et dérivable sur
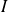et
.
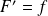Fondamental :
Soit
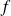une fonction continue par morceaux sur un intervalle
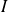de
.
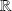Soient
et
sont deux fonctions définies sur un intervalle
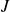de
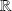à valeurs dans
.
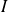Si
et
sont continues sur
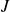, alors la fonction
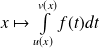est continue sur
.
Si
et
sont dérivables sur
, alors la fonction
est dérivable sur
.
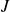En effet :
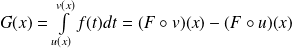où
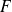est une primitive de
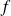sur
.
Et, si
et
sont dérivables :
.
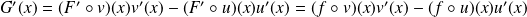Exemple :
Exemple : La fonction
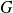définie par :
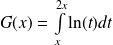est continue et dérivable sur
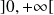et :
.
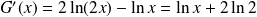On s'intéresse ensuite au cas où la variable apparaît sous le signe
.
Soient
et
deux intervalles de
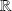et soit
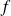une fonction définie sur
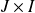à valeurs réelles ou complexes.
On suppose qu'il existe une fonction
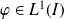telle que :
.
Donc, pour tout
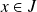, l'intégrale :
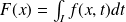est convergente. Donc la fonction
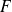est définie sur l'intervalle
.
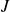Fondamental :
Continuité
On suppose que :
il existe une fonction
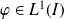telle que :
.pour tout
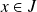, la fonction
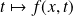est continue par morceaux sur
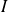.pour tout
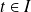, la fonction
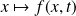est continue sur
.
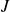Alors la fonction
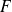définie par :
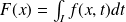est continue sur
.
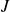Remarque :
Cas particuliers :
Si la fonction
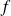est continue sur
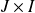, les hypothèses
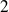et
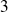sont vérifiées.
Si l'intervalle
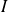est un segment et si la fonction
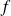est continue sur
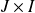, alors la fonction
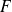est continue sur
.
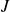Le théorème reste vrai si l'on remplace l'hypothèse
de domination par une hypothèse de domination locale :
Pour tout segment
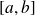inclus dans
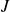, il existe une fonction
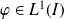telle que :
.
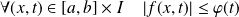C'est une hypothèse moins forte puisque la fonction
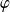dépend alors du segment
.
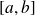Exemple :
Exemple : La fonction
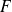définie par :
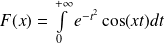est continue sur
.
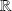En effet :
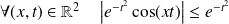. Or la fonction
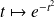est continue et positive sur
.
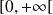De plus elle est intégrable sur
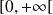car
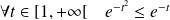qui est intégrable :
.
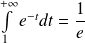Et la fonction
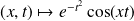est continue sur
, donc vérifie les hypothèses
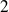et
.
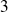Fondamental :
Dérivabilité
On suppose que :
pour tout
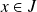, la fonction
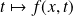est continue par morceaux et intégrable sur
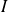.la fonction
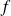possède une dérivée partielle
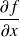.il existe une fonction
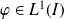telle que
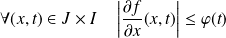.pour tout
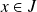, la fonction
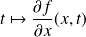est continue par morceaux sur
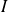,pour tout
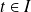, la fonction
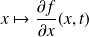est continue sur
.
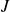Alors la fonction
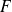définie par :
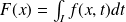est de classe
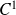sur
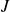et :
.
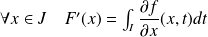Remarque :
Cas particuliers :
Si les fonctions
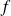et
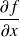sont continues sur
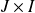, les hypothèses
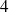et
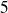sont vérifiées.Si l'intervalle
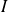est un segment et si les fonctions
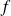et
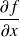sont continues
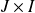, alors la fonction
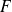est de classe
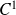sur
.
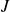Comme précédemment, le théorème reste vrai si l'on remplace l'hypothèse de domination par une hypothèse de domination locale.
Exemple :
Exemple : La fonction
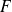définie par :
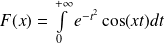est de classe
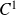sur
.
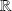En effet, on a vu que pour tout
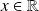, la fonction
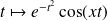est continue et intégrable sur
.
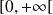La fonction
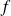définie par :
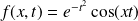admet une dérivée partielle :
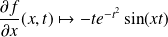qui est continue sur
.
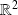De plus :
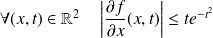. Or la fonction
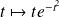est continue et intégrable sur
:
.
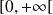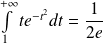Donc
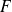est de classe
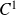sur
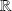et :
.
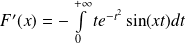