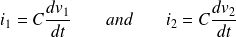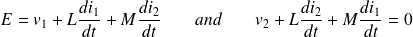Magnetic energy of a two-circuits system
Fondamental : Ohm's generalized law
Two wire circuits
and
are in mutual coupling.
So in the absence of other sources of magnetic field :
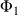is the total magnetic flux through the circuit
and
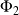the total magnetic flux through the circuit
.
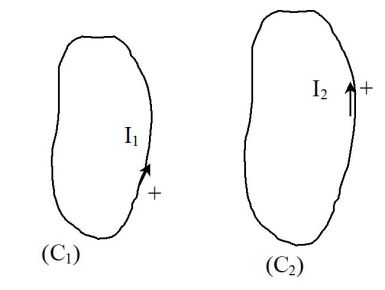
If the two circuits are rigid and still in the laboratory referential, the inductive electromotive forces are :
The voltage differences between the frames of each circuit are :
Fondamental : Magnetic energy of the two-circuits system
The electric power received by the two circuits is :
So :
Finally :
The power dissipated by Joule effect can be recognized :
Another energy can be defined :
This is the magnetic energy of the two-circuits system, in the absence of other sources of magnetic field.
The convention used is that this energy is equal to zero when the currents are equal to zero.
Attention : Energy of the two circuits system
Remarque : Ideal coupling
It is proven that :
We define :
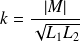
defines the coupling coefficient between the two circuits.
This coefficient has a value ranged between
and
.
The case
, or
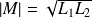, corresponds to the situation where all the magnetic field lines created by one of the two circuits cross the other circuit.
It is the ideal case of perfect coupling.
Exemple : Exercises on coupled circuits
Consider this circuit :
Proper modes research :
Suppose
(free running).
The solutions researched are harmonic and of same pulsation
.
So :
Hence the homogenous system :
This system has one non trivial solution if its determinant is equal to zero :
So :
Hence the two own pulses (with
) :
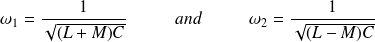
For the first proper mode,
: the two voltages oscillate in accordance.
For the second proper mode,
: the two voltages oscillate in opposite accordance.
The free running corresponds to the linear addition of these two proper modes.
Remarque : Another definition of self-inductance of a circuit
The circuit is a wire loop (or not) without any interaction with another circuit.
To expand the definition of
, we can identify the two expressions of the magnetic energy, hence :
